
���� ���ÿռ������ߡ����桢������λ�ù�ϵ��⣮
��� 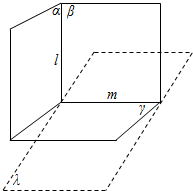 �⣺��������ƽ�е��ж������ô�ֱ��ͬһ��ֱ�ߵ�����ƽ��ƽ�У��ʢ���ȷ��
�⣺��������ƽ�е��ж������ô�ֱ��ͬһ��ֱ�ߵ�����ƽ��ƽ�У��ʢ���ȷ��
��ƽ����ͬһ��ֱ�ߵ�����ƽ��ƽ�л��ཻ���ʢڴ���
��������ƽ�е��ж�����ƽ����ͬһ��ƽ�������ƽ��ƽ�У��ʢ���ȷ��
����ͬһ��ֱ�߳ɵȽǵ�����ƽ��ƽ�л��ཻ���ʢܴ���
��һ��ƽ���ڵ����ֱཻ������һ��ƽ���ڵ����ֱཻ�߷ֱ�ƽ�У���������ƽ��ƽ�л��ཻ���ʢݴ���
��һ��ƽ���Ϲ��ߵ����㵽��һ��ƽ��ľ�����ȣ���������ƽ��ƽ�У��ʢ���
��������ƽ�е��ж�����������ƽ��ֱ��������ƽ���ཻ���õ���������ƽ�У���������ƽ��ƽ�У��ʢ���ȷ��
�൱��ֱ��a��b�ཻʱ�������ڷֱ�ֱ��a��b����������ƽ�е�ƽ�棬�ʢ����
�ᵱ��ֱ��a��b�ཻ�Ҳ���ֱʱ�������ڷֱ�ֱ��a��b���������ഹֱ��ƽ�棬�ʢ����
�����һ������ǵ�����������һ������ǵ�������ֱ�ֱ��
����ͼ�����£��ã��������ഹֱ����Ϊ���£��ý��ߵĶ�ƽ�棬�áͦ��Ҧˡͦ������ã��˼н���ȷ�����ʢ����
�ʴ�Ϊ���٢ۢߣ�
���� ���⿼��������ٵ��жϣ����е��⣬����ʱҪ�������⣬ע��ռ������ߡ����桢������λ�ù�ϵ�ĺ������ã�


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͨ���Ŷ�ij·�ι�·����ʻ�������ٶ�ʵʩ��أ����ٶ���50-90km/h�������г�ȡ150�����з������õ����ݵ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����ٶ���70km/h���µ�������75����
��ͨ���Ŷ�ij·�ι�·����ʻ�������ٶ�ʵʩ��أ����ٶ���50-90km/h�������г�ȡ150�����з������õ����ݵ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����ٶ���70km/h���µ�������75�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��4�� | B�� | ��-1��2�� | C�� | ��1��2�� | D�� | ��2��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com