
【题目】已知向量![]() ,向量
,向量![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,且
,且![]() .
.
(1)求向量![]() ;
;
(2)设向量![]() ,向量
,向量![]() ,其中
,其中![]() ,若
,若![]() ,试求
,试求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() (2)
(2)![]()
【解析】
(1)设向量![]() =(x,y),由已知中向量
=(x,y),由已知中向量![]() =(1,1),向量
=(1,1),向量![]() 与向量
与向量![]() 夹角为
夹角为![]() ,且
,且![]() =﹣1.根据向量数量积的运算法则,可得到关于x,y的方程组,解方程可得向量
=﹣1.根据向量数量积的运算法则,可得到关于x,y的方程组,解方程可得向量![]() 的坐标;(2)由向量
的坐标;(2)由向量![]() =(1,0)向量,其中
=(1,0)向量,其中![]() (
(![]() ,
,![]() ),其中
),其中![]() ,
,![]() ,若
,若![]() =0,我们可以求出
=0,我们可以求出![]() 2的表达式,利用三角函数的性质可得
2的表达式,利用三角函数的性质可得![]() 的取值范围.
的取值范围.
(1)设向量![]() =(x,y),∵向量
=(x,y),∵向量![]() =(1,1),
=(1,1),
则![]() =x+y=﹣1…①
=x+y=﹣1…①![]() =|
=|![]() ||
||![]() |cos
|cos![]() =﹣1,
=﹣1,
即x
解得x=0,y=﹣1或x=﹣1,y=0
故![]() =(﹣1,0),或
=(﹣1,0),或![]() =(0,﹣1),
=(0,﹣1),
(2)∵向量![]() =(1,0),
=(1,0),![]() ⊥
⊥![]() ,则
,则![]() =(0,﹣1),
=(0,﹣1),
又∵向量![]() =(cosx,cos2(
=(cosx,cos2(![]() ﹣
﹣![]() )),
)),
∴![]() +
+![]() =(cosx,cos2(
=(cosx,cos2(![]() ﹣
﹣![]() )﹣1)=(cosx,
)﹣1)=(cosx,![]() ),
),
则|![]() +
+![]() |2=cos2x+
|2=cos2x+![]() =
=![]() cos2x-sinx+
cos2x-sinx+![]() =-
=-![]()
![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
, ![]() |
|![]() +
+![]() |2
|2![]()
故![]() |
|![]() +
+![]() |≤
|≤![]()


科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长分别是
的三边长分别是![]() ,
,![]() ,
,![]() .下列说法正确的是( )
.下列说法正确的是( )
A.以![]() 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为
所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为![]()
B.以![]() 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为
所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为![]()
C.以![]() 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为
所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为![]()
D.以![]() 所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为
所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江心洲有一块如图所示的江边,![]() ,
,![]() 为岸边,岸边形成
为岸边,岸边形成![]() 角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边
角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边![]() 上取两点
上取两点![]() ,用长度为
,用长度为![]() 的围网依托岸边线
的围网依托岸边线![]() 围成三角形
围成三角形![]() (
(![]() ,
,![]() 两边为围网);方案2:在岸边
两边为围网);方案2:在岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,用长度为
,用长度为![]() 的围网
的围网![]() 依托岸边围成三角形
依托岸边围成三角形![]() .请分别计算
.请分别计算![]() ,
,![]() 面积的最大值,并比较哪个方案好.
面积的最大值,并比较哪个方案好.
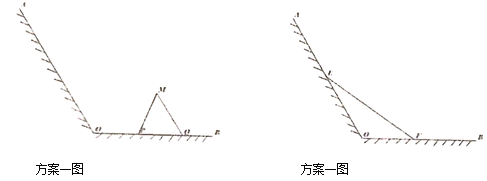
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1,F2,离心率
的左、右焦点分别为F1,F2,离心率![]() ,且椭圆的短轴长为2.
,且椭圆的短轴长为2.
(1)求椭圆的标准方程;
(2)已知直线l1,l2过右焦点F2,且它们的斜率乘积为﹣1,设l1,l2分别与椭圆交于点A,B和C,D.①求AB+CD的值;②设AB的中点M,CD的中点为N,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,使AC=a,得到三棱锥A-BCD,如图所示.

(1)当a=2时,求证:AO⊥平面BCD.
(2)当二面角A-BD-C的大小为120°时,求二面角A-BC-D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,纵、横坐标都是整数的点称为整点。请设计一种方法将所有的整点染色,每一个整点染成白色、红色或黑色中的一种颜色,使得
(1)每一种颜色的点出现在无穷多条平行于横轴的直线上;
(2)对于任意白点![]() 、红点
、红点![]() 及黑点
及黑点![]() ,总可以找到一个红点
,总可以找到一个红点![]() ,使
,使![]() 为一平行四边形。证明你设计的方法符合上述要求。
为一平行四边形。证明你设计的方法符合上述要求。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com