
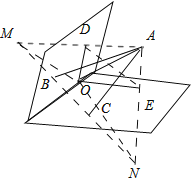
【题目】已知二面角α﹣l﹣β为60°,在其内部取点A,在半平面α,β内分别取点B,C.若点A到棱l的距离为1,则△ABC的周长的最小值为_____.
【答案】![]()
【解析】
作A关于平面α和β的对称点M,N,交α和β与D,E,连接MN,AM,AN,DE,根据对称性三角形ADC的周长为AB+AC+BC=MB+BC+CN,当四点共线时长度最短,结合对称性和余弦定理求解.
作A关于平面α和β的对称点M,N,交α和β与D,E,
连接MN,AM,AN,DE,
根据对称性三角形ABC的周长为AB+AC+BC=MB+BC+CN,
当M,B,C,N共线时,周长最小为MN设平面ADE交l于,O,连接OD,OE,
显然OD⊥l,OE⊥l,
∠DOE=60°,∠MOA+∠AON=240°,OA=1,
∠MON=120°,且OM=ON=OA=1,根据余弦定理,
故MN2=1+1﹣2×1×1×cos120°=3,
故MN![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
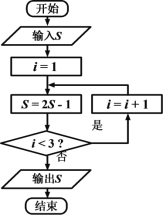
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了了解市民搭乘公共交通工具的出行情况,收集并整理了2017年全年每月公交和地铁载客量的数据,绘制了下面的折线图:
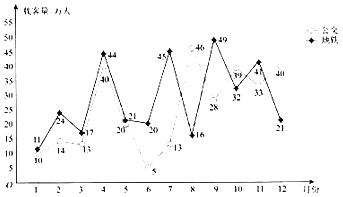
根据该折线图,下列结论错误的是( )
A.全年各月公交载客量的极差为41B.全年各月地铁载客量的中位数为22.5
C.7月份公交与地铁的载客量相差最多D.全年地铁载客量要小于公交载客量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为别为
的左、右焦点为别为![]() 、
、![]() ,且过点
,且过点![]() 和
和![]() .
.
(1)求椭圆的标准方程;
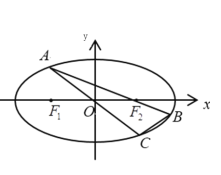
(2)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,
,![]() 的延长线与椭圆交于点
的延长线与椭圆交于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=2,点P在棱DF上.
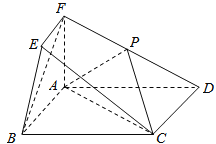
(1)若P是DF的中点,求异面直线BE与CP所成角的余弦值;
(2)若二面角D﹣AP﹣C的正弦值为![]() ,求PF的长度.
,求PF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com