
分析 (1)把b=1-$\frac{a}{2}$代入函数解析式,求出导函数,分a=0,a>0和a<0三类求得h(x)在[0,1]上的最大值φ(a);
(2)F(x)=f(x)-g(x)=ex-2x-b,求得F′(x)=ex-2,由F(x)在(0,ln2)上单调递减,在(ln2,+∞)上单调递增,把F(x)=ex-2x-b在[0,2]上恰有两个相异实根转化为$\left\{\begin{array}{l}{F(0)=1-b≥0}\\{F(ln2)=2-2ln2-b<0}\\{F(2)={e}^{2}-4≥0}\end{array}\right.$,求解不等式组可得实数b的取值范围.
解答 解:(1)b=1-$\frac{a}{2}$时,h(x)=${e}^{x}(\frac{a}{2}x+1-\frac{a}{2})$,∴h′(x)=${e}^{x}(\frac{a}{2}x+1)$.
①当a=0时,h′(x)=ex>0,h(x)在[0,1]上为增函数,此时φ(a)=e;
②当a>0时,h′(x)=${e}^{x}•\frac{a}{2}(x+\frac{2}{a})$,h(x)在(-$\frac{2}{a},+∞$)上为增函数,
故h(x)在[0,1]上为增函数,此时φ(a)=h(1)=e;
③当a<0时,h′(x)=${e}^{x}•\frac{a}{2}(x+\frac{2}{a})$,h(x)在(-∞,$-\frac{2}{a}$)上为增函数,在(-$\frac{2}{a}$,+∞)上为减函数,
若0$<-\frac{2}{a}<1$,即a<-2时,故h(x)在[0,$-\frac{2}{a}$]上为增函数,在[$-\frac{2}{a},1$]上为减函数,
此时φ(a)=h(-$\frac{2}{a}$)=${e}^{-\frac{2}{a}}(-1+b)=-\frac{a}{2}•{e}^{-\frac{2}{a}}$.
若-$\frac{2}{a}≥1$,即-2≤a<0时,h(x)在[0,1]上为增函数,则此时φ(a)=h(1)=e,
综上所述:φ(a)=$\left\{\begin{array}{l}{-\frac{a}{2}•{e}^{-\frac{2}{a}},a<-2}\\{e,a≥-2}\end{array}\right.$;
(2)F(x)=f(x)-g(x)=ex-2x-b,F′(x)=ex-2,
∴F(x)在(0,ln2)上单调递减,在(ln2,+∞)上单调递增,
∴F(x)=ex-2x-b在[0,2]上恰有两个相异实根,
?$\left\{\begin{array}{l}{F(0)=1-b≥0}\\{F(ln2)=2-2ln2-b<0}\\{F(2)={e}^{2}-4≥0}\end{array}\right.$,解得2-2ln2<b≤1.
∴实数b的取值范围是b∈(2-2ln2,1].
点评 本题考查利用导数研究函数的单调性,考查利用导数求函数在闭区间上的最值,体现了数学转化思想方法与分类讨论的数学思想方法,属难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,-1,4) | B. | (9,1,4) | C. | (3,1,1) | D. | (1,-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{x={t^2}}\\{y={t^4}}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=sint}\\{y={{sin}^2}t}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=t}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=t}\\{y={t^2}}\end{array}}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -$\frac{3}{2}$ | C. | $\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
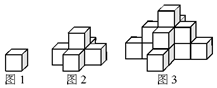 图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第六个叠放的图形中,小正方体木块总数就是( )
图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第六个叠放的图形中,小正方体木块总数就是( )| A. | 25 | B. | 66 | C. | 91 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
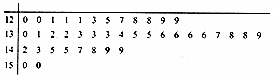 在高三某次数学测试中,40名优秀学生的成绩如图所示:
在高三某次数学测试中,40名优秀学生的成绩如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com