
【题目】某市房管局为了了解该市市民![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间买二手房情况,首先随机抽样其中
月期间买二手房情况,首先随机抽样其中![]() 名购房者,并对其购房面积
名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图
)进行了一次调查统计,制成了如图![]() 所示的频率分布直方图,接着调查了该市
所示的频率分布直方图,接着调查了该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间当月在售二手房均价
月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图
(单位:万元/平方米),制成了如图![]() 所示的散点图(图中月份代码
所示的散点图(图中月份代码![]() 分别对应
分别对应![]() 年
年![]() 月至
月至![]() 年
年![]() 月).
月).
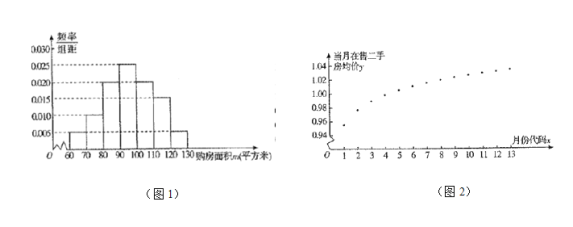
(1)试估计该市市民的购房面积的中位数![]() ;
;
(2)现采用分层抽样的方法从购房面积位于![]() 的
的![]() 位市民中随机抽取
位市民中随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求这
人,求这![]() 人的购房面积恰好有一人在
人的购房面积恰好有一人在![]() 的概率;
的概率;
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值如下表所示:
,并得到一些统计量的值如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.006050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出![]() 年
年![]() 月份的二手房购房均价(精确到
月份的二手房购房均价(精确到![]() )
)
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(参考公式)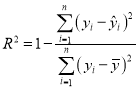
【答案】(1) ![]() ; (2)
; (2) ![]() (3) 模型
(3) 模型![]() 的拟合效果更好;
的拟合效果更好;![]() 万元/平方米
万元/平方米
【解析】
(1)先由频率分布直方图,求出前三组频率和与前四组频率和,确定中位数出现在第四组,根据中位数两侧的频率之和均为![]() ,即可得出结果;
,即可得出结果;
(2)设从位于![]() 的市民中抽取
的市民中抽取![]() 人,从位于
人,从位于![]() 的市民中抽取
的市民中抽取![]() 人,根据分层抽样,求出
人,根据分层抽样,求出![]() ,
,![]() ;由列举法确定从
;由列举法确定从![]() 人中随机抽取
人中随机抽取![]() 人所包含的基本事件个数,以及满足条件的基本事件个数,进而可求出概率;
人所包含的基本事件个数,以及满足条件的基本事件个数,进而可求出概率;
(3)根据题中数据,分别求出两种模型对应的相关指数,比较大小,即可确定拟合效果;再由确定的模型求出预测值即可.
(1)由频率分布直方图,可得,前三组频率和为![]() ,
,
前四组频率和为![]() ,
,
故中位数出现在第四组,且![]() .
.
(2)设从位于![]() 的市民中抽取
的市民中抽取![]() 人,从位于
人,从位于![]() 的市民中抽取
的市民中抽取![]() 人,
人,
由分层抽样可知:![]() ,则
,则![]() ,
,![]()
在抽取的![]() 人中,记
人中,记![]() 名位于
名位于![]() 的市民为
的市民为![]() ,
,![]() ,
,![]() ,位于
,位于![]() 的市民为
的市民为![]() 则所有抽样情况为:
则所有抽样情况为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6种.
共6种.
而其中恰有一人在口![]() 的情况共有
的情况共有![]() 种,故所求概率
种,故所求概率![]()
(3)设模型![]() 和
和![]() 的相关指数分别为
的相关指数分别为![]() ,
,![]() ,
,
则![]() ,
,![]() 显然
显然![]()
故模型![]() 的拟合效果更好.
的拟合效果更好.
由![]() 年
年![]() 月份对应的代码为
月份对应的代码为![]() ,
,
则![]() 万元/平方米
万元/平方米


科目:高中数学 来源: 题型:
【题目】点![]() 是曲线
是曲线![]() :
:![]() 上的一个动点,曲线
上的一个动点,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 是坐标原点,①
是坐标原点,①![]() ;②
;②![]() 的面积为定值;③曲线
的面积为定值;③曲线![]() 上存在两点
上存在两点![]() ,
,![]() 使得
使得![]() 是等边三角形;④曲线
是等边三角形;④曲线![]() 上存在两点
上存在两点![]() ,
,![]() 使得
使得![]() 是等腰直角三角形,其中真命题的个数是( )
是等腰直角三角形,其中真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为了解高二学生每天自主学习中国古典文学的时间,随机抽取了高二男生和女生各50名进行问卷调查,其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”,否则为“非古文迷”,调查结果如下表:
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
参考公式: ,其中
,其中![]()
参考数据:
| 0.500 | 0.400 | 0.250 | 0.050 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
(1)根据上表数据判断能否有60%的把握认为“古文迷”与性别有关?
(2)现从调查的女生中按分层抽样的方法抽出5人进行理科学习时间的调查,求所抽取的5人中“古文迷”和“非古文迷”的人数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,的焦点为
,的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,
,![]() 两点,抛物线在点
两点,抛物线在点![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,两条切线的交点为
,两条切线的交点为![]() .
.
(1)证明:![]() ;
;
(2)若![]() 的外接圆
的外接圆![]() 与抛物线
与抛物线![]() 有四个不同的交点,求直线
有四个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:①在区间
满足:①在区间![]() 上单调递减;②存在常数
上单调递减;②存在常数![]() ,使其值域为
,使其值域为![]() ,则称函数
,则称函数![]() 为
为![]() 的“渐近函数”.
的“渐近函数”.
(1)设![]() ,若
,若![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 取值范围;
取值范围;
(2)证明:函数![]() 是函数
是函数![]() ,
,![]() 的渐近函数,并求此时实数
的渐近函数,并求此时实数![]() 的值;
的值;
(3)若函数![]() ,
,![]() ,
,![]() ,证明:当
,证明:当![]() 时,
时,![]() 不是
不是![]() 的渐近函数.
的渐近函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与坐标原点![]() 重合,极轴与
重合,极轴与![]() 轴非负半轴重合,
轴非负半轴重合,![]() 是曲线
是曲线![]() 上任一点
上任一点![]() 满足
满足![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的平面直角坐标方程;
的平面直角坐标方程;
(2)将曲线![]() 向右平移
向右平移![]() 个单位后得到曲线
个单位后得到曲线![]() ,设曲线
,设曲线![]() 与直线
与直线![]() (
(![]() 为参数)相交于
为参数)相交于![]() 、
、![]() 两点,记点
两点,记点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex-alnx(无理数e=2.718…).
(1)若f(x)在(0,1)单调递减,求实数a的取值范围;
(2)当a=-1时,设g(x)=x(f(x)-xex)-x3+x2-b,若函数g(x)存在零点,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“柯西不等式”是由数学家柯西在研究数学分析中的“流数”问题时得到的,但从历史的角度讲,该不等式应当称为柯西﹣﹣布尼亚科夫斯基﹣﹣施瓦茨不等式,因为正是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式推广到完善的地步,在高中数学选修教材4﹣5中给出了二维形式的柯西不等式:(a2+b2)(c2+d2)≥(ac+bd)2当且仅当ad=bc(即![]() )时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数
)时等号成立.该不等式在数学中证明不等式和求函数最值等方面都有广泛的应用.根据柯西不等式可知函数![]() 的最大值及取得最大值时x的值分别为( )
的最大值及取得最大值时x的值分别为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com