
【题目】已知椭圆C:![]() (
(![]() ).若
).若![]() ,
,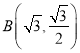 ,
,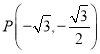 ,
,![]() 四点中有且仅有三点在椭面C上.
四点中有且仅有三点在椭面C上.
(1)求椭圆C的标准方程;
(2)设O为坐标原点,F为椭圆C的右焦点,过点F的直线l分别与椭圆C交于M,N两点,![]() ,求证:直线
,求证:直线![]() ,
,![]() 关于x轴对称.
关于x轴对称.
科目:高中数学 来源: 题型:
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为![]() 万元/辆和
万元/辆和![]() 万元/辆的
万元/辆的![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)从![]() 和
和![]() 的车型中各随机抽取
的车型中各随机抽取![]() 车,以
车,以![]() 表示这
表示这![]() 车中使用寿命不低于
车中使用寿命不低于![]() 年的车数,求
年的车数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据公司要求,采购成本由出租公司负责,平均每辆出租车每年上交公司![]() 万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这
万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这![]() 辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
附: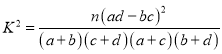 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,
,![]() 为
为![]() 的中点.
的中点.
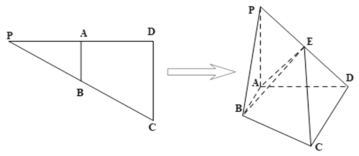
(1)证明:![]() 平面
平面![]() ;
;
(2)当正视图方向与向量![]() 的方向相同时,此时
的方向相同时,此时![]() 的正视图的面积为
的正视图的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点O为坐标原点,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,离心率为
(a>b>0)的左、右焦点分别为F1,F2,离心率为![]() ,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为
,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为![]() .
.
(1)求椭圆C的标准方程;
(2)过点H(-2,0)的直线交椭圆C于A,B两点,若AF1⊥BF1,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2a=2bcosC+csinB.
(Ⅰ)求tanB;
(Ⅱ)若C![]() ,△ABC的面积为6,求BC.
,△ABC的面积为6,求BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年9月24日,阿贝尔奖和菲尔兹奖双料得主、英国著名数学家阿蒂亚爵士宣布自己证明了黎曼猜想,这一事件引起了数学界的震动,在1859年,德国数学家黎曼向科学院提交了题目为《论小于某值的素数个数》的论文并提出了一个命题,也就是著名的黎曼猜想.在此之前,著名数学家欧拉也曾研究过这个问题,并得到小于数字![]() 的素数个数大约可以表示为
的素数个数大约可以表示为![]() 的结论(素数即质数,
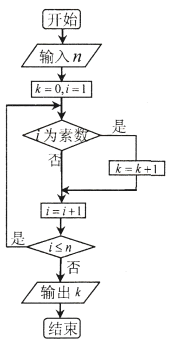
的结论(素数即质数,![]() ).根据欧拉得出的结论,如下流程图中若输入
).根据欧拉得出的结论,如下流程图中若输入![]() 的值为
的值为![]() ,则输出
,则输出![]() 的值应属于区间( )
的值应属于区间( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣sinx(a∈R).
(1)当![]() 时,f(x)
时,f(x)![]() 0恒成立,求正实数a的取值范围;
0恒成立,求正实数a的取值范围;
(2)当a≥1时,探索函数F(x)![]() f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,港口A在港口O的正东100海里处,在北偏东方向有条直线航道OD,航道和正东方向之间有一片以B为圆心,半径为![]() 海里的圆形暗礁群(在这片海域行船有触礁危险),其中OB=
海里的圆形暗礁群(在这片海域行船有触礁危险),其中OB=![]() 海里,tan∠AOB=
海里,tan∠AOB=![]() ,cos∠AOD=
,cos∠AOD=![]() ,现一艘科考船以
,现一艘科考船以![]() 海里/小时的速度从O出发沿OD方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A出发,并沿直线方向行驶与科考船恰好相遇.
海里/小时的速度从O出发沿OD方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A出发,并沿直线方向行驶与科考船恰好相遇.
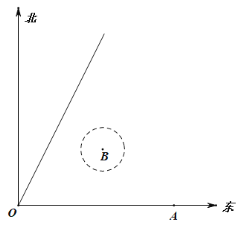
(1)若快艇立即出发,判断快艇是否有触礁的危险,并说明理由;
(2)在无触礁危险的情况下,若快艇再等x小时出发,求x的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com