练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．设直线l为抛物线y2=2px（p＞0）的焦点，且交抛物线于A，B两点，交其准线于C点，已知|AF|=4，$\overrightarrow{CB}$=2$\overrightarrow{BF}$，则p=2．

    分析 分别过A、B作准线的垂线，利用抛物线定义将A、B到焦点的距离转化为到准线的距离，结合已知比例关系，在直角三角形ADC中求线段PF长度即可得p值，进而可得方程．

    解答 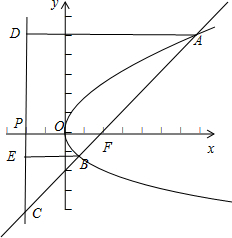解：如图过A作AD垂直于抛物线的准线，垂足为D，
    过B作BE垂直于抛物线的准线，垂足为E，P为准线与x轴的焦点，
    由抛物线的定义，|BF|=|BE|，|AF|=|AD|=4，
    ∵|BC|=2|BF|，∴|BC|=2|BE|，∴∠DCA=30°
    ∴|AC|=2|AD|=8，∴|CF|=8-4=4，
    ∴|PF|=$\frac{1}{2}$|CF|═2，即p=|PF|=2，
    故答案为：2

    点评 本题考查抛物线的定义及其应用，抛物线的几何性质，过焦点的弦的弦长关系，转化化归的思想方法，属中档题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．设集合A={x|x2-3x+a=0}，B={x|x2+b=0}，若A∩B={2}，求A∪B．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知向量$\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（-1，1），$\overrightarrow{c}$=（4，2），若$\overrightarrow{c}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$，λ、μ∈R，则λ+μ=（　　）
    A．-2B．-1C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．在等差数列{an}中，Sn是该数列的前n项和，已知a4+a8=4，则S11+a6=（　　）
    A．12B．16C．24D．48

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

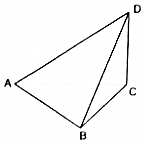    9．如图所示，在三棱锥D-ABC中，AB=BC=CD=2，AD=2$\sqrt{3}$，∠ABC=90°，平面ACD⊥平面ABC．
    （1）求证：AB⊥BD；
    （2）求点C到平面ABD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．过抛物线y2=4x的焦点F的直线交抛物线于A，B两点，点O是原点，若|AF|=5，则△AOF的面积为$\frac{5}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

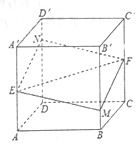    6．如图所示，正方体ABCD-A′B′C′D′的棱长为1，E、F分别是棱是AA′，CC′的中点，过直线EF的平面分别与棱BB′，DD′交于M，N，设BM=x，x∈[0，1]，给出以下四种说法：
    （1）平面MENF⊥平面BDD′B′；
    （2）当且仅当x=$\frac{1}{2}$时，四边形MENF的面积最小；
    （3）四边形MENF周长L=f（x），x∈[0，1]是单调函数；
    （4）四棱锥C′-MENF的体积V=h（x）为常函数，以上说法中正确的为（　　）
    A．（2）（3）B．（1）（3）（4）C．（1）（2）（3）D．（1）（2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知不等式ax2+5x+b＜0的解集为{x|-3＜x＜2}，则不等式bx2+5x+a＞0的解集为（-$\frac{1}{3}$，$\frac{1}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．一个几何体的三视图如图所示，则该几何体的表面积为（　　）
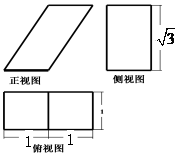
    A．2+4$\sqrt{3}$B．4+4$\sqrt{3}$C．8+2$\sqrt{3}$D．6+2$\sqrt{3}$

    查看答案和解析>>

    同步练习册答案