
【题目】函数![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 为偶函数,当
为偶函数,当![]() 时,
时,![]() ,若函数
,若函数![]() 恰有一个零点,则实数
恰有一个零点,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:根据条件判断函数的周期性和对称性,求出函数在一个周期内的解析式,利用转化法进行求解即可.
详解:∵f(x)是定义在R上的奇函数,且f(x﹣1)为偶函数,
∴f(﹣x﹣1)=f(x﹣1)=﹣f(x+1),
即f(x)=﹣f(x+2),
则f(x+4)=﹣f(x+2)=f(x),即函数f(x)的周期是4,
∵f(x﹣1)为偶函数,∴f(x﹣1)关于x=0对称,
则f(x)关于x=﹣1对称,同时也关于x=1对称,
若x∈[﹣1,0],则﹣x∈[0,1],
此时f(﹣x)=![]() =﹣f(x),则f(x)=﹣
=﹣f(x),则f(x)=﹣![]() ,x∈[﹣1,0],
,x∈[﹣1,0],
若x∈[﹣2,﹣1],x+2∈[0,1],
则f(x)=﹣f(x+2)=﹣![]() ,x∈[﹣2,﹣1],
,x∈[﹣2,﹣1],
若x∈[1,2],x﹣2∈[﹣1,0],
则f(x)=﹣f(x﹣2)=![]() =
=![]() ,x∈[1,2],
,x∈[1,2],
作出函数f(x)的图象如图:
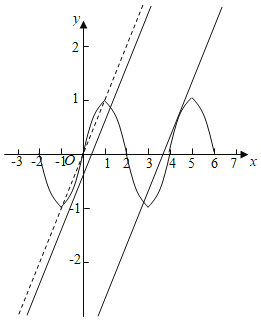
由数g(x)=f(x)﹣x﹣b=0得f(x)=x+b,
由图象知当x∈[﹣1,0]时,由﹣![]() =x+b,平方得x2+(2b+1)x+b2=0,
=x+b,平方得x2+(2b+1)x+b2=0,
由判别式△=(2b+1)2﹣4b2=0得4b+1=0,得b=﹣![]() ,此时f(x)=x+b有两个交点,
,此时f(x)=x+b有两个交点,
当x∈[4,5],x﹣4∈[0,1],则f(x)=f(x﹣4)=![]() ,
,
由![]() =x+b,平方得x2+(2b﹣1)x+4+b2=0,
=x+b,平方得x2+(2b﹣1)x+4+b2=0,
由判别式△=(2b﹣1)2﹣16﹣4b2=0得4b=﹣15,得b=﹣![]() ,此时f(x)=x+b有两个交点,
,此时f(x)=x+b有两个交点,
则要使此时f(x)=x+b有一个交点,则在[0,4]内,b满足﹣![]() <b<﹣
<b<﹣![]() ,
,
即实数b的取值集合是4n﹣![]() <b<4n﹣
<b<4n﹣![]() ,
,
即4(n﹣1)+![]() <b<4(n﹣1)+
<b<4(n﹣1)+![]() ,
,
令k=n﹣1,
则4k+![]() <b<4k+
<b<4k+![]() ,
,
故选:D.


科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 作不与
作不与![]() 轴重合的直线
轴重合的直线![]() ,设
,设![]() 与圆
与圆![]() 相交于
相交于![]() 两点,与椭圆相交于
两点,与椭圆相交于![]() 两点,当
两点,当![]() 且
且![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才,对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:

例如,表中运动协调能力良好且逻辑思维能力一般的学生有![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
(III)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,设运动协调能力或逻辑思维能力优秀的学生人数为
位,设运动协调能力或逻辑思维能力优秀的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 和
和![]() ,点
,点![]() 在椭圆上,且
在椭圆上,且![]() 的面积为
的面积为![]() .
.
(1)求该椭圆的标准方程;
(2)过该椭圆的左顶点![]() 作两条相互垂直的直线分别与椭圆相交于不同于点
作两条相互垂直的直线分别与椭圆相交于不同于点![]() 的两点
的两点![]() 、
、![]() ,证明:动直线
,证明:动直线![]() 恒过
恒过![]() 轴上一定点.
轴上一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() .已知点
.已知点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是边长为4的等边三角形.
是边长为4的等边三角形.
(1)求![]() 的值;
的值;
(2)若直线![]() 是过定点
是过定点![]() 的一条直线,且与抛物线
的一条直线,且与抛物线![]() 交于
交于![]() 两点,过
两点,过![]() 作
作![]() 的垂
的垂
线与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com