
(1)求双曲线方程;
(2)若过B(1,0)点的直线l交双曲线C上支一点M,下支一点N,且4MB=5BN,求直线l的方程.
解:(1)若双曲线焦点在x轴上,?
∵渐近线方程为y=±![]() x,?
x,?
∴双曲线方程设为![]() =1(b>0). ?
=1(b>0). ?
设动点P的坐标为(x,y),?
则|AP|=![]() .?
.?
∵x∈(-∞,-2b]∪[2b,+∞),?
∴①若x=4≤2b,即b≥2,则当x=2b时,|AP|Min=|2b-5|=![]() .?
.?
解得b=![]() (b=
(b=![]() <2应舍去),?
<2应舍去),?
此时双曲线方程为 -
- =1. ?
=1. ?
②若x=4>2b,即b<2,则当x=4时,|AP|Min=![]()
∴b2=-1,无解. ?
若双曲线焦点在y轴上,双曲线方程可设为![]() =1(b>0),?
=1(b>0),?
∴|PA|=![]() .?
.?
∵x∈R,∴x=4时,|PA|Min=![]() .∴b=1.?
.∴b=1.?
此时双曲线方程为y2-![]() =1.?
=1.?
综上所述,双曲线方程为 -
-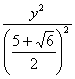 =1或y2-
=1或y2-![]() =1. ?
=1. ?
(2)由(1)知,双曲线方程为y2-![]() =1,设直线l方程为x=ky+1.?
=1,设直线l方程为x=ky+1.?
由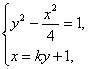 得(4-k2)y2-2ky-5=0,依题意
得(4-k2)y2-2ky-5=0,依题意

![]() -
-![]() <0.
<0.
∴-2<k<2.设M(x1,y1),y1>0,N(x2,y2),y2<0,?
由韦达定理得y1+y2=![]() ; ①?
; ①?
y1·y2=-![]() . ②?
. ②?
∵4![]() =5
=5![]() ,∴-4y1=5y2. ③
,∴-4y1=5y2. ③
由③得y1=-![]() y2,代入①②得?
y2,代入①②得?
-![]() y2=
y2=![]() >0, ④?
>0, ④?
-![]() y22=-
y22=-![]() , ⑤?
, ⑤?
即ln![]() <
<![]() =1+
=1+![]() (n≥2).?
(n≥2).?
∴ln![]() +ln
+ln![]() +ln
+ln![]() +…+ln
+…+ln![]() <(1+
<(1+![]() )+(1+
)+(1+![]() )+…+(1+
)+…+(1+![]() )=n+
)=n+![]() +
+![]() +…+
+…+![]() .?
.?
综上所证,![]() +
+![]() +…+
+…+![]() <lnn<n+
<lnn<n+![]() +
+![]() +…+
+…+![]() (n∈N*且n≥2)成立. ?
(n∈N*且n≥2)成立. ?
由④⑤消去y2,解得k=![]() (k=-
(k=-![]() <0,舍).?
<0,舍).?
∴直线l的方程为x=![]() y+1.
y+1.


科目:高中数学 来源: 题型:
| 3 |
| 2 |
A、y=±
| ||||
| B、y=±x | ||||
C、x=±
| ||||
D、x=±
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com