
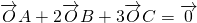 ,则S△AOC:S△ABC=________.
,则S△AOC:S△ABC=________.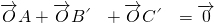 ,从而O是△AB′C′的重心,利用S△AOC′=S△B′OC′=S△AOB′=
,从而O是△AB′C′的重心,利用S△AOC′=S△B′OC′=S△AOB′= S△AB′C′,即可得到S△AOC:S△BOC:S△AOB=2:1:3,从而可得结论.
S△AB′C′,即可得到S△AOC:S△BOC:S△AOB=2:1:3,从而可得结论.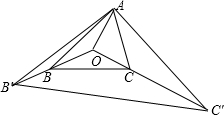 解:延长OB至B',使OB'=2OB;延长OC至C',使OC'=3OC,则
解:延长OB至B',使OB'=2OB;延长OC至C',使OC'=3OC,则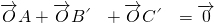
 S△AB′C′,
S△AB′C′, S△AOC′,S△BOC=
S△AOC′,S△BOC= S△B′′OC′,S△AOB=
S△B′′OC′,S△AOB= S△AOB′,
S△AOB′,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com