练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某地区某农产品近几年的产量统计如表：

    年份

    2012

    2013

    2014

    2015

    2016

    2017

    年份代码t

    1

    2

    3

    4

    5

    6

    年产量y(万吨)

    6.6

    6.7

    7

    7.1

    7.2

    7.4

    （Ⅰ）根据表中数据，建立关于的线性回归方程；

    （Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量.

    附:对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为：，.(参考数据:，计算结果保留小数点后两位）

    【答案】（1）．

    （2）预测2019年该地区该农产品的年产量约为万吨．

    【解析】

    （1）先求得，然后利用线性回归方程的计算公式计算得到的值，从而求得线性回归方程.（2）将代入（1）求得的回归直线方程，来求年产量的预测值.

    （1）由题意可知：，

    ，

    ，

    ∴，

    又，

    ∴y关于t的线性回归方程为．

    （2）由（1）可得，当年份为2019年时，年份代码，此时，

    所以，可预测2019年该地区该农产品的年产量约为万吨．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，正方体ABCD－A′B′C′D′的棱长为a，连接A′C′，A′D，A′B，BD，BC′，C′D，得到一个三棱锥.求：

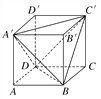
    (1)三棱锥A′－BC′D的表面积与正方体表面积的比值；

    (2)三棱锥A′－BC′D的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设双曲线的两支为(如图)，正三角形PQR的三顶点位于此双曲线上。

    （1）求证：P、Q、R不能都在双曲线的同一支上；

    （2）设P(-1，-1)在上，Q、R在上。求顶点Q、R的坐标。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)若函数的图象与轴无交点，求的取值范围；

    (2)若函数在上存在零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知角α＝45°，

    (1)在－720°～0°范围内找出所有与角α终边相同的角β；

    (2)设集合，判断两集合的关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四面体ABCD中，O、E分别是BD、BC的中点，

    （Ⅰ）求证：平面BCD；

    （Ⅱ）求点E到平面ACD的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—4：坐标系与参数方程

    已知曲线的参数方程为（为参数），以平面直角坐标系的原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （Ⅰ）求曲线的直角坐标方程及曲线上的动点到坐标原点的距离的最大值；

    （Ⅱ）若曲线与曲线相交于，两点，且与轴相交于点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数恰有一个零点，求实数的取值范围；

    （2）设关于的方程的两个不等实根，求证：（其中为自然对数的底数）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直角梯形ABDC中，，，，，.

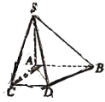
    （1）若S是直角梯形ABDC所在平面外一点，画出平面SBD和平面SAC的交线，并说明理由；

    （2）直角梯形ABDC绕直线AC所在直线旋转一周所得几何体名称是什么?并求出其体积.

    查看答案和解析>>

    同步练习册答案