
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求证:
时,求证: ![]() ,并指出等号成立的条件;
,并指出等号成立的条件;
(Ⅱ)求证:对任意实数![]() ,总存在实数
,总存在实数![]() ,有
,有![]() .
.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析
【解析】试题分析:
(Ⅰ)构造新函数![]() ,利用导函数研究函数的单调性可得
,利用导函数研究函数的单调性可得![]() ,据此即可证得
,据此即可证得![]() .
.
(Ⅱ)原问题等价于![]() .然后分类讨论当
.然后分类讨论当![]() 时和当
时和当![]() 时的情况即可证得题中的结论.
时的情况即可证得题中的结论.
试题解析:
(Ⅰ)设![]()
![]() .
.
∵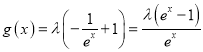 ,
,
∴当![]() 时,
时, ![]() ,故
,故![]() 递增;当
递增;当![]() 时,
时, ![]() ,故
,故![]() 递减.
递减.
因此, ![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
(Ⅱ)解法一:“存在实数![]() ,有
,有![]() ”等价于
”等价于![]() .
.
注意到![]() .∵
.∵![]() ,
,
∴当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() 成立;
成立;
当![]() 时,令
时,令![]() ,得
,得![]() ,∴
,∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
若![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上递增,故
上递增,故![]() 成立;
成立;
若![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上递增,故
上递增,故![]() 成立;
成立;
若![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
故![]() 成立.
成立.
综上所述,对任意实数![]() ,总存在实数
,总存在实数![]() ,有
,有![]() .
.
解法二:①当![]() 时,
时, ![]() 在区间
在区间![]() 上递增,则
上递增,则![]() ,
,
②当![]() 时,由(Ⅰ)可知
时,由(Ⅰ)可知![]() ;
;
③当![]() 时,由(Ⅰ)可知
时,由(Ⅰ)可知![]()
综上,对任意实数![]() ,总存在实数
,总存在实数![]() ,有
,有![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若椭圆的离心率为![]() ,且点
,且点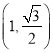 在椭圆上,①求椭圆的方程;
在椭圆上,①求椭圆的方程;
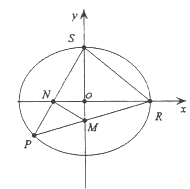
②设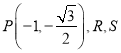 分别为椭圆
分别为椭圆![]() 的右顶点和上顶点,直线
的右顶点和上顶点,直线![]() 和
和![]() 与
与![]() 轴和
轴和![]() 轴相交于点
轴相交于点![]() ,求直线
,求直线![]() 的方程;
的方程;
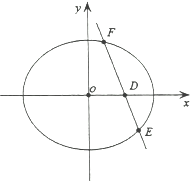
(2)设 ![]() 过
过![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 均在
均在![]() 的右侧,
的右侧, ![]() ,求椭圆离心率的取值范围.
,求椭圆离心率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在双曲线 ![]() 中,F1 , F2分别是左右焦点,A1 , A2 , B1 , B2分别为双曲线的实轴与虚轴端点,若以A1A2为直径的圆总在菱形F1B1F2B2的内部,则此双曲线
中,F1 , F2分别是左右焦点,A1 , A2 , B1 , B2分别为双曲线的实轴与虚轴端点,若以A1A2为直径的圆总在菱形F1B1F2B2的内部,则此双曲线 ![]() 离心率的取值范围是( )
离心率的取值范围是( )
A.![]()
B.[ ![]() ,+∞)
,+∞)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各小题中,P是q的充要条件的是(08年山东理改编)
1)p:m<﹣2或m>6;q:y=x2+mx+m+3有两个不同的零点.
2)p: ![]() =1,q:y=f(x)是偶函数.
=1,q:y=f(x)是偶函数.
3)p:cosα=cosβ,q:tanα=tanβ.
4)p:A∩B=A,q:CUBCUA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=2|x﹣m|﹣1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列等式:32=52﹣42 , 52=132﹣122 , 72=252﹣242 , 92=412﹣402 , …照此规律,第n个等式为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() (a>0,b>0).
(a>0,b>0).
(1)当a=b=1时,证明:f(x)不是奇函数;
(2)设f(x)是奇函数,求a与b的值;
(3)在(2)的条件下,试证明函数f(x)的单调性,并解不等式f(1﹣m)+f(1+m2)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com