
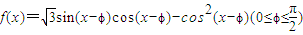 为偶函数.
为偶函数.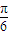 个单位(纵坐标不变),得到函数g(x)的图象,求方程
个单位(纵坐标不变),得到函数g(x)的图象,求方程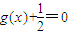 的解集.
的解集.
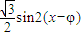 -
-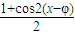 =
=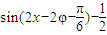 ,
,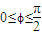 且,∴-2φ
且,∴-2φ =
= ,k∈Z,解得φ=
,k∈Z,解得φ=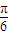 ,
, =-cos2x
=-cos2x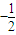 ,
, ≤x≤kπ,
≤x≤kπ, ,kπ](k∈Z),
,kπ](k∈Z), 个单位,得到函数g(x)的图象,则g(x)=-cos(2x-
个单位,得到函数g(x)的图象,则g(x)=-cos(2x-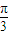 )
) ,
, 得,-cos(2x-
得,-cos(2x- )=0,即cos(2x-
)=0,即cos(2x-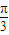 )=0,解得2x-
)=0,解得2x-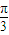 =
= (k∈Z),
(k∈Z),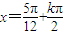 (k∈Z),
(k∈Z),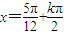 (k∈Z)}.
(k∈Z)}.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2012-2013学年山东省青岛市高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 为偶函数.
为偶函数. ,判断λ与E的关系;
,判断λ与E的关系; (m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m,n的值.
(m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m,n的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省湛江市吴川市川西中学高一(下)期中数学试卷(解析版) 题型:解答题
 为偶函数,且函数y=f(x)图象的两相邻对称轴的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴的距离为 .
. 个单位后,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,得到函数y=g(x)的图象,求g(x)的单调递减区间. ,使不等式f(x)<m成立,求实数m的取值范围.
,使不等式f(x)<m成立,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:正定中学2010高三下学期第一次考试(数学理) 题型:解答题
(本小题满分10分)
已知函数 为偶函数,且其图象上相邻两对称轴之间的距离为
为偶函数,且其图象上相邻两对称轴之间的距离为 .
.
(I)求函数 的表达式。
的表达式。
(II)若 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com