
【题目】已知数列{an}是公差为2的等差数列,数列{bn}满足 ![]() ,若n∈N*时,anbn+1﹣bn+1=nbn .
,若n∈N*时,anbn+1﹣bn+1=nbn .
(Ⅰ)求{bn}的通项公式;
(Ⅱ)设cn=anbn , 求{cn}的前n项和Sn .
【答案】解:(I)∵数列{bn}满足 ![]() ,anbn+1﹣bn+1=nbn . ∴n=1时,可得a1b2﹣b2=b1 , 即
,anbn+1﹣bn+1=nbn . ∴n=1时,可得a1b2﹣b2=b1 , 即 ![]() ﹣
﹣ ![]() =1,解得a1=3.
=1,解得a1=3.
∴an=3+2(n﹣1)=2n+1.
∴[(2n+1)﹣1]bn+1=nbn , 可得bn+1= ![]() bn ,
bn ,
∴数列{bn}是等比数列,公比为 ![]() .
.
∴bn= ![]() .
.
(II)cn=anbn=(2n+1)× ![]() .
.
∴{cn}的前n项和Sn= ![]() +7×
+7× ![]() +…+(2n+1)×
+…+(2n+1)× ![]() .
.
∴ ![]() =
= ![]() +…+(2n﹣1)×
+…+(2n﹣1)× ![]() +(2n+1)×
+(2n+1)× ![]() ,
,
∴ ![]() =3+
=3+ ![]() ﹣(2n+1)×
﹣(2n+1)× ![]() =1+
=1+ 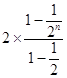 ﹣(2n+1)×
﹣(2n+1)× ![]() ,
,
∴Tn=10﹣ ![]()
【解析】(I)由数列{bn}满足 ![]() ,anbn+1﹣bn+1=nbn . n=1时,可得a1b2﹣b2=b1 , 即
,anbn+1﹣bn+1=nbn . n=1时,可得a1b2﹣b2=b1 , 即 ![]() ﹣
﹣ ![]() =1,解得a1 . 可得an=2n+1.代入anbn+1﹣bn+1=nbn . 利用等比数列的通项公式即可得出.(II)cn=anbn=(2n+1)×
=1,解得a1 . 可得an=2n+1.代入anbn+1﹣bn+1=nbn . 利用等比数列的通项公式即可得出.(II)cn=anbn=(2n+1)× ![]() .利用“错位相减法”与等比数列的求和公式即可得出.
.利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系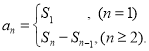 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】高速公路为人民出行带来极大便利,但由于高速上车速快,一旦出事故往往导致生命或财产的重大损失,我国高速公路最高限速120km/h,最低限速60km/h.
(1)当驾驶员以120 千米/小时速度驾车行驶,驾驶员发现前方有事故,以原车速行驶大约需要0.9秒后才能做出紧急刹车,做出紧急刹车后,车速依v(t)= ![]() ﹣
﹣ ![]() t(t:秒,v(t):米/秒)规律变化直到完全停止,求驾驶员从发现前方事故到车辆完全停止时,车辆行驶的距离;(取ln5=1.6)
t(t:秒,v(t):米/秒)规律变化直到完全停止,求驾驶员从发现前方事故到车辆完全停止时,车辆行驶的距离;(取ln5=1.6)
(2)国庆期间,高速免小车通行费,某人从襄阳到曾都自驾游,只需承担油费.已知每小时油费v(元)与车速有关,w= ![]() +40(v:km/h),高速路段必须按国家规定限速内行驶,假定高速上为匀速行驶,高速上共行驶了S千米,当高速上行驶的这S千米油费最少时,求速度v应为多少km/h?
+40(v:km/h),高速路段必须按国家规定限速内行驶,假定高速上为匀速行驶,高速上共行驶了S千米,当高速上行驶的这S千米油费最少时,求速度v应为多少km/h?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是定义在
是定义在 ![]() 上的可导函数
上的可导函数 ![]() 的导数,对任意
的导数,对任意 ![]()
![]() ,且
,且 ![]() ,且
,且 ![]() ,都有
,都有 ![]() ,
, ![]() ,
, ![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A.![]() 的增区间为
的增区间为 ![]()
B.![]() 在
在 ![]() =3处取极小值,在
=3处取极小值,在 ![]() =-1处取极大值??
=-1处取极大值??
C.![]() 有3个零点
有3个零点
D.![]() 无最大值也无最小值
无最大值也无最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={(x,y)|y=x2+2bx+1},B={(x,y)|y=2a(x+b)},且A∩B是单元素集合,若存在a<0,b<0使点P∈{(x,y)|(x﹣a)2+(y﹣b)2≤1},则点P所在的区域的面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,则对任意实数a、b,若a+b≥0则( )
,则对任意实数a、b,若a+b≥0则( )
A.f(a)+f(b)≤0
B.f(a)+f(b)≥0
C.f(a)﹣f(b)≤0
D.f(a)﹣f(b)≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a是常数,对任意实数x,不等式|x+1|﹣|2﹣x|≤a≤|x+1|+|2﹣x|都成立.
(Ⅰ)求a的值;
(Ⅱ)设m>n>0,求证:2m+ ![]() ≥2n+a.
≥2n+a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}各项为正数,且a2=4a1 , an+1= ![]() +2an(n∈N*)
+2an(n∈N*)
(I)证明:数列{log3(1+an)}为等比数列;
(Ⅱ)令bn=log3(1+a2n﹣1),数列{bn}的前n项和为Tn , 求使Tn>345成立时n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,a2=3,若|an+1﹣an|=2n(n∈N*),且{a2n﹣1}是递增数列、{a2n}是递减数列,则 ![]()
![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F1、F2为双曲线C:x2﹣ ![]() =1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,∠MF1F2=30°.
=1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,∠MF1F2=30°.
(1)求双曲线C的方程;
(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线,垂足分别为P1、P2 , 求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com