
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,当
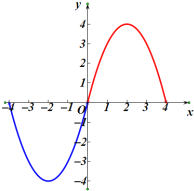
上的奇函数,当![]() 时,
时,![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】∵f(x)是定义在[﹣4,4]上的奇函数,
∴当x=0时,f(0)=0,
下面求x∈[﹣4,0)时的f(x)的表达式,
设x∈[﹣4,0),则﹣x∈(0,4],
又∵当x>0时,f(x)=﹣x2+4x,
∴f(﹣x)=﹣(﹣x)2+4(﹣x)=﹣x2﹣4x,
又f(x)是定义在[﹣4,4]上的奇函数,
∴f(x)=﹣f(﹣x)=x2+4x,
∴f(x)=![]() ,
,
令f(x)=0,解得x=﹣4或0或4,
当x∈[﹣4,0]时,不等式f[f(x)]<f(x),
即(x2+4x)2+4(x2+4x)<x2+4x,
化简得(x2+4x)2+3(x2+4x)<0,
解得x∈(﹣4,﹣3)∪(﹣1,0);
当x∈(0,4]时,不等式f[f(x)]<f(x),
即﹣(﹣x2+4x)2+4(﹣x2+4x)<﹣x2+4x,
化简得﹣(﹣x2+4x)2+3(﹣x2+4x)<0,
解得x∈(1,3);
综上所述,x∈(﹣4,﹣3)∪(﹣1,0)∪(1,3),
故选:D.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,且0<x1<x2 , 给出下列命题: ① ![]() <1
<1
②x2f(x1)<x1f(x2)
③当lnx>﹣1时,x1f(x1)+x2f(x2)>2x2f(x1)
④x1+f(x1)<x2+f(x2)
其中正确的命题序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各两张,让孩子从盒子里任取3张卡片,按卡片上的最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量X的分布列及数学期望;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图. 
(Ⅰ)求图中x的值;
(Ⅱ)已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过左焦点F且垂直于x轴的弦长为1.
,过左焦点F且垂直于x轴的弦长为1.
(I)求椭圆C的标准方程;
(Ⅱ)点P(m,0)为椭圆C的长轴上的一个动点,过点P且斜率为 ![]() 的直线l交椭圆C于A,B两点,问:|PA|2+|PB|2是否为定值?若是,求出这个定值并证明,否则,请说明理由.
的直线l交椭圆C于A,B两点,问:|PA|2+|PB|2是否为定值?若是,求出这个定值并证明,否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,
, ![]() ,使得
,使得![]() 的解集恰好是
的解集恰好是![]() ,若存在,求出
,若存在,求出![]() ,
, ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线C的参数方程: ![]() ,直线l的参数方程为
,直线l的参数方程为 ![]() .
.
(1)若直线l与曲线C只有一个公共点,求实数a;
(2)若点P,Q分别为直线l与曲线C上的动点,若 ![]() ,求实数a.
,求实数a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com