
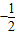 x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=
x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=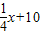 ,(0<x≤40,x∈N+),在后40天内价格为g2(x)=
,(0<x≤40,x∈N+),在后40天内价格为g2(x)=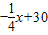 (40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.
(40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.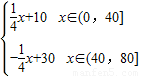 ,而销售量满足f (x)=
,而销售量满足f (x)= x+40(0<x≤80,x∈N+),
x+40(0<x≤80,x∈N+),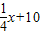 )(
)(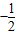 x+40)=-
x+40)=- (x+40)(x-80)=-
(x+40)(x-80)=- (x-20)2+450≤450,(0<x≤40,x∈N+)(当且仅当x=20时取等号)
(x-20)2+450≤450,(0<x≤40,x∈N+)(当且仅当x=20时取等号)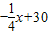 )(
)(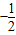 x+40)=
x+40)= (x-120)(x-80)=
(x-120)(x-80)= (x-100)2-50<
(x-100)2-50< (40-100)2-50=400
(40-100)2-50=400

 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省邢台一中高一(上)第一次月考数学试卷(解析版) 题型:解答题
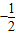 x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=
x+40(0<x≤80,x∈N+),在前40天内价格为g1(x)=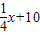 ,(0<x≤40,x∈N+),在后40天内价格为g2(x)=
,(0<x≤40,x∈N+),在后40天内价格为g2(x)=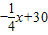 (40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.
(40<x≤80,x∈N+).求这种商品哪天的销售额最大,并求最大值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省南充高中高一(上)第一次月考数学试卷(解析版) 题型:解答题
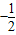 x+40(0<x≤40,x∈N+),在40天内价格为g (x)=
x+40(0<x≤40,x∈N+),在40天内价格为g (x)=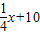 ,(0<x≤40,x∈N+).求这种商品哪天的销售额最大,并求最大值.
,(0<x≤40,x∈N+).求这种商品哪天的销售额最大,并求最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com