
【题目】现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ![]() .类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 . 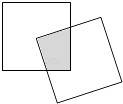
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为x(m),三块种植植物的矩形区域的总面积为S(m2). 
(1)求S关于x的函数关系式;
(2)求S的最大值,及此时长X的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为an的一组正三角形AnBn﹣1Bn的底边Bn﹣1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为2的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则a的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线C1:y2=2px与椭圆C2: ![]() 在第一象限的交点为B,O为坐标原点,A为椭圆的右顶点,△OAB的面积为
在第一象限的交点为B,O为坐标原点,A为椭圆的右顶点,△OAB的面积为 ![]() .
. 
(1)求抛物线C1的方程;
(2)过A点作直线L交C1于C、D两点,求线段CD长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双流中学校运动会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位: ![]() ),身高在175
),身高在175![]() 以上(包括175
以上(包括175![]() )定义为“高个子”,身高在175
)定义为“高个子”,身高在175![]() 以 下(不包括175
以 下(不包括175![]() )定义为“非高个子”.
)定义为“非高个子”.

(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率?
(2)若从身高180![]() 以上(包括180
以上(包括180![]() )的志愿者中选出男、女各一人,求这两人身高相差5
)的志愿者中选出男、女各一人,求这两人身高相差5![]() 以上的概率.
以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家订了一份报纸,暑假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
(1)根据图中的数据信息,求出众数![]() 和中位数
和中位数![]() (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间![]() 在上午
在上午![]() 至
至![]() 之间,而送报人每天在
之间,而送报人每天在![]() 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件![]() )的概率.
)的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:设a,b∈R,则“a+b>4”是“a>2且b>2”的必要不充分条件;命题q:若 ![]() <0,则
<0,则 ![]() ,
, ![]() 夹角为钝角,在命题①p∧q;②¬p∨¬q;③p∨¬q;④¬p∨q中,真命题是( )
夹角为钝角,在命题①p∧q;②¬p∨¬q;③p∨¬q;④¬p∨q中,真命题是( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com