
分析 (1)求导y′=1-$\frac{1}{{x}^{2}}$<1,从而可判断函数y=x+$\frac{1}{x}$图象上各点处切线的斜率都小于1.
(2)令y′=1-$\frac{1}{{x}^{2}}$=0得x=±1,从而由导数的几何意义求切线方程.
解答 解:(1)证明:∵y=x+$\frac{1}{x}$,
∴y′=1-$\frac{1}{{x}^{2}}$<1,
即对函数y=x+$\frac{1}{x}$定义域内的任一x,其导数值都小于1,
由导数的几何意义可知,
函数y=x+$\frac{1}{x}$图象上各点处切线的斜率都小于1.
(2)令y′=1-$\frac{1}{{x}^{2}}$=0,得x=±1,
当x=1时,y=1+1=2;
当x=-1时,y=-2,
∴曲线y=x+$\frac{1}{x}$的斜率为0的切线有两条,其切点分别为(1,2)与(-1,-2),
切线方程分别为y=2或y=-2.
点评 本题考查了导数的几何意义与导数的综合应用,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>2 | B. | a≥2 | C. | a<2 | D. | a≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
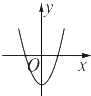 B、
B、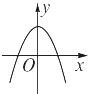 C、
C、 D、
D、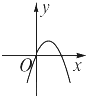
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com