
【题目】建设生态文明,是关系人民福祉,关乎民族未来的长远大计.某市通宵营业的大型商场,为响应节能减排的号召,在气温超过![]() 时,才开放中央空调降温,否则关闭中央空调.如图是该市夏季一天的气温(单位:
时,才开放中央空调降温,否则关闭中央空调.如图是该市夏季一天的气温(单位:![]() )随时间(
)随时间(![]() ,单位:小时)的大致变化曲线,若该曲线近似的满足函数
,单位:小时)的大致变化曲线,若该曲线近似的满足函数![]() 关系.
关系.
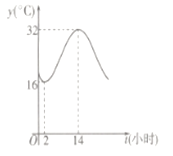
(1)求函数![]() 的表达式;
的表达式;
(2)请根据(1)的结论,判断该商场的中央空调应在本天内何时开启?何时关闭?
科目:高中数学 来源: 题型:
【题目】在公差为d的等差数列{an}中,已知a1=10,且a1 , 2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的16%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金y(单位:万元),销售利润x(单位:万元)
(1)写出该公司激励销售人员的奖励方案的函数模型;
(2)如果业务员老张获得5.6万元的奖金,那么他的销售利润是多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点
(a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点 ![]() .
.
(1)求椭圆C的离心率:
(2)设过点A(0,2)的直线l与椭圆C交于M,N两点,点Q是线段MN上的点,且 ![]() ,求点Q的轨迹方程.
,求点Q的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 为n个正数
为n个正数![]() 的“均倒数”.已知正项数列{an}的前n项的“均倒数”为
的“均倒数”.已知正项数列{an}的前n项的“均倒数”为![]() .
.
(1)求数列{an}的通项公式.
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若4
,若4![]() <
<![]() 对一切
对一切![]() 恒成立试求实数m的取值范围.
恒成立试求实数m的取值范围.
(3)令![]() ,问:是否存在正整数k使得
,问:是否存在正整数k使得![]() 对一切
对一切![]() 恒成立,如存在求出k值,否则说明理由.
恒成立,如存在求出k值,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为终点的向量分别为 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;以D为起点,其余顶点为终点的向量分别为
;以D为起点,其余顶点为终点的向量分别为 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .若m、M分别为(
.若m、M分别为( ![]() +
+ ![]() +
+ ![]() )(
)( ![]() +
+ ![]() +
+ ![]() )的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
)的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
A.m=0,M>0
B.m<0,M>0
C.m<0,M=0
D.m<0,M<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. 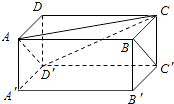
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com