
【题目】党的十九大报告明确指出要坚决打赢脱贫攻坚战,让贫困人口和贫困地区同全国一道进入全面小康社会,要动员全党全国全社会力量,坚持精准扶贫、精准脱贫,确保到2020年我国现行标准下农村贫困人口实现脱贫.现有扶贫工作组到某山区贫困村实施脱贫工作.经摸底排查,该村现有贫困农户100户,他们均从事水果种植,2017年底该村平均每户年纯收入为1万元,扶贫工作组一方面请有关专家对水果进行品种改良,提高产量;另一方面,抽出部分农户从事水果包装、销售工作,其户数必须小于种植的户数.从2018年初开始,若该村抽出![]() 户(
户(![]() ,
,![]() )从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高
)从事水果包装、销售.经测算,剩下从事水果种植农户的年纯收入每户平均比上一年提高![]() ,而从事包装销售农户的年纯收入每户平均为
,而从事包装销售农户的年纯收入每户平均为![]() 万元.(参考数据:
万元.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
(1)至2018年底,该村每户年均纯收入能否达到1.32万元?若能,请求出从事包装、销售的户数;若不能,请说明理由;
(2)至2020年底,为使从事水果种植农户能实现脱贫(即每户(水果种植农户)年均纯收入不低于1.6万元),至少要抽出多少户从事包装、销售工作?
【答案】(1)从事包装、销售的户数为16,20,24,28,32,36户时能达到每户平均纯收入1.32万元.(2)16户
【解析】
(1)假设至2018年底每户年均纯收入能达到1.32万元,由已知可得每户的平均收入为: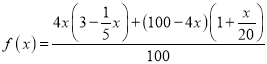 ,令
,令![]() ,解一元二次不等式即可求解.
,解一元二次不等式即可求解.
(2)由已知可得至2020年底,种植户每户平均收入为![]() ,
,![]() ,解不等式即可.
,解不等式即可.
解:(1)假设至2018年底每户年均纯收入能达到1.32万元,由已知可得:
每户的平均收入为: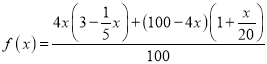 ,
,
令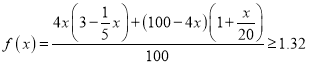 ,
,
化简,得![]() ,解得:
,解得:![]() ,
,
因为![]() ,
,![]() , 且
, 且![]() ,可得:
,可得:![]() ,
,
所以,当从事包装、销售的户数为16,20,24,28,32,36户时能达到每户平均纯收入1.32万元.
(2)由已知可得:至2020年底,种植户每户平均收入为![]() ,
,
令![]() ,得:
,得:![]() ,
,
由题所给数据,知:![]() ,所以,
,所以,![]() ,
,
所以,![]() 的最小值为4,
的最小值为4,![]() ,
,
即至少抽出16户从事包装、销售工作.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数,
(t为参数,![]() ).
).
(1)写出直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,直线l的倾斜角![]() ,P点坐标为
,P点坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 在左、右顶点分别为
在左、右顶点分别为![]() 、
、![]() ,左焦点为
,左焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 和
和![]() 均不在坐标轴上),直线
均不在坐标轴上),直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() ,求证:
,求证:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() 的中点.
的中点.
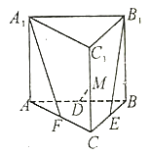
(1)证明:直线![]() 与
与![]() 共面;并求其所成角的余弦值;
共面;并求其所成角的余弦值;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,以
的上、下顶点,以![]() 为直径作圆
为直径作圆![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() (
(![]() 为坐标原点)的面积;
为坐标原点)的面积;
(2)若点![]() 、
、![]() 分别在直线
分别在直线![]() 、
、![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)证明:对任意实数![]() ,函数
,函数![]() 的图象与直线
的图象与直线![]() 最多只有一个交点;
最多只有一个交点;
(3)设![]() 若函数
若函数![]() 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某城市在2019年1月份至10月份各月最低温与最高温(℃)的数据表,已知该城市的各月最低温与最高温具有相关关系,根据该表,则下列结论错误的是( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
最高温 | 5 | 9 | 9 | 11 | 17 | 24 | 27 | 30 | 31 | 21 |
最低温 |
|
| 1 |
| 7 | 17 | 19 | 23 | 25 | 10 |
A.最低温与最高温为正相关
B.每月最低温与最高温的平均值在前8个月逐月增加
C.月温差(最高温减最低温)的最大值出现在1月
D.1至4月温差(最高温减最低温)相对于7至10月,波动性更大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com