已知f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0 成立,则a=( )
A.a≥2
B.a≤4
C.a≥4
D.a=4
【答案】
分析:这类不等式在某个区间上恒成立的问题,可转化为求函数最值的问题,本题要分三类:①x=0,②x>0,③x<0等三种情形,当x=0时,不论a取何值,f(x)≥0都成立;当x>0时有a≥
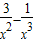
,可构造函数g(x)=
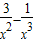
,然后利用导数求g(x)的最大值,只需要使a≥g(x)
max,同理可得x<0时的a的范围,从而可得a的值.
解答:解:若x=0,则不论a取何值,f(x)≥0都成立;
当x>0即x∈(0,1]时,f(x)=ax
3-3x+1≥0可化为:a≥
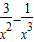
设g(x)=
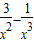
,则g′(x)=
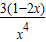
,
所以g(x)在区间(0,

]上单调递增,在区间[

,1]上单调递减,
因此g(x)
max=g(

)=4,从而a≥4;
当x<0即x∈[-1,0)时,f(x)=ax
3-3x+1≥0可化为:a≤
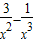
,
g(x)=
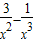
在区间[-1,0)上单调递增,
因此g(x)
min=g(-1)=4,从而a≤4,综上a=4.
故选D.
点评:本题考查的是含参数不等式的恒成立问题,考查分类讨论,转化与化归的思想方法,利用导数和函数的单调性求函数的最大值,最小值等知识与方法.在讨论时,容易漏掉x=0的情形,因此分类讨论时要特别注意该问题的解答.

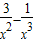 ,可构造函数g(x)=
,可构造函数g(x)=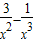 ,然后利用导数求g(x)的最大值,只需要使a≥g(x)max,同理可得x<0时的a的范围,从而可得a的值.
,然后利用导数求g(x)的最大值,只需要使a≥g(x)max,同理可得x<0时的a的范围,从而可得a的值.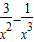
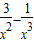 ,则g′(x)=
,则g′(x)=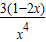 ,
, ]上单调递增,在区间[
]上单调递增,在区间[ ,1]上单调递减,
,1]上单调递减, )=4,从而a≥4;
)=4,从而a≥4;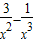 ,
,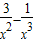 在区间[-1,0)上单调递增,
在区间[-1,0)上单调递增,

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案