
满足性质:“对于区间(1,2)上的任意 ,
,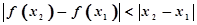 恒成立”的函数叫Ω函数,则下面四个函数中,属于Ω函数的是( )
恒成立”的函数叫Ω函数,则下面四个函数中,属于Ω函数的是( )
A.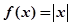 | B. | C. | D. |
C
解析试题分析:首先分析题目的新定义满足:“对于区间(1,2)上的任意实数x1,x2(x1≠x2),|f(x2)-f(x1)|<|x2-x1|恒成立”,则称f(x)为优美函数,要求选择Ω函数.故需要对4个选项代入不等式|f(x2)-f(x1)|<|x2-x1|分别验证是否成立即可得到答案
在区间(1,2)上的任意实数x1,x2(x1≠x2),分别验证下列4个函数.
对于A:f(x)=|x|,|f(x2)-f(x1)|=||x2|-|x1||=|x2-x1|(因为故x1和x2大于0)故对于等于号不满足,故不成立.
对于C:f(x)=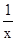 ,|f(x2)-f(x1)|=|
,|f(x2)-f(x1)|=|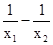 |=|
|=|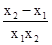 |<|x2-x1|(因为x1,x2在区间(1,2)上,故x1x2大于1)故成立.
|<|x2-x1|(因为x1,x2在区间(1,2)上,故x1x2大于1)故成立.
对于B:f(x)=2x,|f(x2)-f(x1)|=|2x2-2x1|<|x2-x1|.不成立.
对于D:f(x)=x2,|f(x2)-f(x1)|=|x22-x12|=(x2+x1)|x2-x1|>|x2-x1|不成立,故选C.
考点:本试题主要考查了新定义的理解和应用问题.涉及到绝对值不等式的应用.属于中档题目。
点评:解决该试题的关键需要对题目概念做认真分析再做题。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:单选题
对实数a和b,定义运算“⊕”:a⊕b= 设函数f(x)=(x2-2)⊕(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
设函数f(x)=(x2-2)⊕(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
A.(-∞,-2]∪ | B.(-∞,-2]∪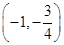 |
C.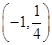 ∪ ∪ | D.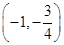 ∪ ∪ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com