
分析 (1)对于甲:{xn}为“s~不减数列”?xs<xs+1<xs+2<…,对于乙:{xn}为“t~不减数列”?xt<xt+1<xt+2<…,从而判断出“甲是乙的充分条件”是假命题.
(2)由反函数知y=f(x)=$\frac{1}{2-x}$,从而可得an+1=$\frac{1}{2-{a}_{n}}$,从而可判断出a2<a1,且a2<a3<a4<a5<…,从而求得.
(3)假设存在实数λ使得{xn}为“$\frac{1}{2}$f(f($\frac{4}{3}$))~不减数列”,解$\frac{1}{2}$f(f($\frac{4}{3}$))=1,从而可得{xn}是单调递增数列,故当n≥3时,xn-xn-1=2n-1+(-1)nλ($\frac{3}{{2}^{n}}$+2)>0,即(-1)nλ>-$\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$,从而讨论以确定λ的取值范围.
解答 解:(1)对于甲:{xn}为“s~不减数列”?xs<xs+1<xs+2<…,
对于乙:{xn}为“t~不减数列”?xt<xt+1<xt+2<…,
∵s,t为正整数,且s>t,
∴乙⇒甲,显然甲推不出乙,
故甲是乙的必要条件,从而“甲是乙的充分条件”是假命题.
(2)∵函数y=f(x)与函数y=-$\frac{1}{x}$+2的图象关于直线y=x对称,
∴函数y=f(x)与函数y=-$\frac{1}{x}$+2互为反函数,
故y=f(x)=$\frac{1}{2-x}$,
由an+1=f(an)得an+1=$\frac{1}{2-{a}_{n}}$,
由a1=3得a2=-1<1,
假设ak=<1(k≥2),
则ak+1=$\frac{1}{2-{a}_{k}}$<1,
即n≥2时,an<1;
于是an+1-an=$\frac{1}{2-{a}_{n}}$-an=$\frac{({a}_{n}-1)^{2}}{2-{a}_{n}}$>0(n≥2),
故a2<a1,且a2<a3<a4<a5<…,
故n0的最小值为2.
(3)假设存在实数λ使得{xn}为“$\frac{1}{2}$f(f($\frac{4}{3}$))~不减数列”,
∵$\frac{1}{2}$f(f($\frac{4}{3}$))=1,∴{xn}是单调递增数列,
∵cosnπ=(-1)n,且f($\frac{4}{3}$)=$\frac{3}{2}$,
∴yn=$\left\{\begin{array}{l}{\frac{3}{2},n=1}\\{(-1)^{n}(\frac{1}{{2}^{n}}+1),n≥2}\end{array}\right.$,
又∵xn=2n+λyn,
故当n≥3时,xn-xn-1=2n-1+(-1)nλ($\frac{3}{{2}^{n}}$+2)>0,(-1)nλ>-$\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$,
若n为大于或等于4的偶数,则有λ>-$\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$恒成立,
故λ>(-$\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$)max=-$\frac{{2}^{4-1}}{\frac{3}{{2}^{4}}+2}$=-$\frac{128}{35}$,故λ>-$\frac{128}{35}$,
若n为大于或等于3的奇数,则有λ<$\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$恒成立,故λ<($\frac{{2}^{n-1}}{\frac{3}{{2}^{n}}+2}$)min=$\frac{{2}^{3-1}}{\frac{3}{{2}^{3}}+2}$=$\frac{32}{19}$,故λ<$\frac{32}{19}$,
又当n=2时,x2-x1=(4+$\frac{5}{4}$λ)-(2+$\frac{3}{2}$λ)>0,故λ<8;
综上可知,λ的取值范围为(-$\frac{128}{35}$,$\frac{32}{19}$).
点评 本题考查了分类讨论的思想应用及学生学习能力,同时考查了数学归纳法的应用.


科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}•\overrightarrow{{C_1}A}={a^2}$ | B. | $\overrightarrow{AB}•\overrightarrow{{A_1}{C_1}}=\sqrt{2}{a^2}$ | C. | $\overrightarrow{BC}•\overrightarrow{{A_1}D}={a^2}$ | D. | $\overrightarrow{AB}•\overrightarrow{{C_1}{A_1}}={a^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
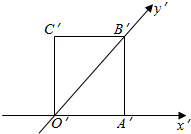 如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )
如图的正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的面积为( )| A. | 2$\sqrt{2}$cm2 | B. | 1cm2 | C. | 4$\sqrt{2}$cm2 | D. | $\frac{\sqrt{2}}{4}$cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\sqrt{2}-1,\;\sqrt{2}+1]$ | B. | $[\sqrt{2}-1,\;\sqrt{2}]$ | C. | $[\sqrt{2},\;\sqrt{2}+1]$ | D. | $[2-\sqrt{2},\;2+\sqrt{2}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com