
分析 (1)由条件化简整理,再由等比数列的定义和通项公式,即可得到所求;
(2)运用分析法证明,即证2≤(1+$\frac{1}{n}$)n<3,再由二项式定理展开,运用不等式的性质和等比数列的求和公式,即可得证.
解答 解:(1)由n[fn($\frac{k+1}{n}$)-fn($\frac{k}{n}$)]=[fn($\frac{k}{n}$)-1]fn($\frac{k+1}{n}$),
可得(n+1)fn($\frac{k+1}{n}$)-nfn($\frac{k}{n}$)=fn($\frac{k+1}{n}$)fn($\frac{k}{n}$),
即$\frac{n+1}{{f}_{n}(\frac{k}{n})}$-$\frac{n}{{f}_{n}(\frac{k+1}{n})}$=1,
即有(n+1)ak-nak+1=1可得n(ak+1-1)=(n+1)(ak-1),
即$\frac{{a}_{k+1}-1}{{a}_{k}-1}$=1+$\frac{1}{n}$,
由n为定值,则数列{ak-1}是以a0-1为首项,1+$\frac{1}{n}$为公比的等比数列,
∴ak-l=(a0-1)(1+$\frac{1}{n}$)k,
由于a0=$\frac{1}{{f}_{n}(0)}$=2,
故ak=1+(1+$\frac{1}{n}$)k(k=0,1,2,…,n-1);
(2)由ak=$\frac{1}{{f}_{n}(\frac{k}{n})}$,结合(1)可得fn(1)=$\frac{1}{{a}_{n}}$=$\frac{1}{1+(1+\frac{1}{n})^{n}}$,
要证$\frac{1}{4}$<fn(1)≤$\frac{1}{3}$,即证3≤1+(1+$\frac{1}{n}$)n<4,
即证2≤(1+$\frac{1}{n}$)n<3,
由(1+$\frac{1}{n}$)n=1+${C}_{n}^{1}$•$\frac{1}{n}$+${C}_{n}^{2}$•$\frac{1}{{n}^{2}}$+…+${C}_{n}^{n}$•$\frac{1}{{n}^{n}}$=1+1+…≥2;
又(1+$\frac{1}{n}$)n=1+${C}_{n}^{1}$•$\frac{1}{n}$+${C}_{n}^{2}$•$\frac{1}{{n}^{2}}$+…+${C}_{n}^{n}$•$\frac{1}{{n}^{n}}$
=1+1+$\frac{n(n-1)}{2{n}^{2}}$+…+$\frac{n(n-1)…2•1}{n!{n}^{n}}$
≤1+1+$\frac{1}{2!}$+…+$\frac{1}{n!}$<1+1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$
=2+$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=3-($\frac{1}{2}$)n<3.
故原不等式$\frac{1}{4}$<fn(1)$≤\frac{1}{3}$成立.
点评 本题考查数列的通项的求法,注意运用构造法,运用等比数列的定义和通项,考查不等式的证明,注意运用分析法和二项式定理,结合不等式的性质,考查推理能力,属于难题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
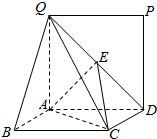 如图,矩形ABCD所在的平面与正方形ADPQ所在的平面相互垂直,E是QD的中点.
如图,矩形ABCD所在的平面与正方形ADPQ所在的平面相互垂直,E是QD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 2+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,3} | B. | {-1,0,1,2,3} | C. | {-1,0,3} | D. | {-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=sinx•cosx的最大值为1 | |
| B. | 将y=sin(2x+$\frac{π}{4}$)图象向右平移$\frac{π}{8}$个单位,再将所得图象上各点的横坐标变为原来的2倍,得到正弦函数y=sinx的图象 | |
| C. | 函数f(x)=1-$\frac{1}{x}$在(-∞,0)上是减函数 | |
| D. | 函数f(x)=$\frac{1}{x}$-x的图象关于y轴对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com