
【题目】已知函数f(x)=alnx+(x﹣c)|x﹣c|,a<0,c>0.
(1)当a=﹣ ![]() ,c=
,c= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当c= ![]() +1时,若f(x)≥
+1时,若f(x)≥ ![]() 对x∈(c,+∞)恒成立,求实数a的取值范围;
对x∈(c,+∞)恒成立,求实数a的取值范围;
(3)设函数f(x)的图象在点P(x1 , f(x1))、Q(x2 , f(x2))两处的切线分别为l1、l2 . 若x1= ![]() ,x2=c,且l1⊥l2 , 求实数c的最小值.
,x2=c,且l1⊥l2 , 求实数c的最小值.
【答案】
(1)解:函数 ![]() ,求导得
,求导得 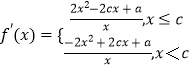
当 ![]() ,
, ![]() 时,
时, 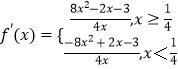 ,
,
若 ![]() ,则
,则 ![]() 恒成立,所以f(x)在
恒成立,所以f(x)在 ![]() 上单调减;
上单调减;
若 ![]() ,则
,则 ![]() ,令f′(x)=0,解得
,令f′(x)=0,解得 ![]() 或
或 ![]() (舍),
(舍),
当 ![]() 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在 ![]() 上单调减;
上单调减;
当 ![]() 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在 ![]() 上单调增.
上单调增.
所以函数f(x)的单调减区间是 ![]() ,单调增区间是
,单调增区间是 ![]()
(2)解:当x>c, ![]() 时,
时, ![]() ,而
,而 ![]() ,所以
,所以
当c<x<1时,f′(x)<0,f(x)在(c,1)上单调减;
当x>1时,f′(x)>0,f(x)在(1,+∞)上单调增.
所以函数f(x)在(c,+∞)上的最小值为 ![]() ,
,
所以 ![]() 恒成立,解得a≤﹣1或a≥1,
恒成立,解得a≤﹣1或a≥1,
又由 ![]() ,得a>﹣2,所以实数a的取值范围是(﹣2,﹣1]
,得a>﹣2,所以实数a的取值范围是(﹣2,﹣1]
(3)解:由l1⊥l2知, ![]() ,而
,而 ![]() ,则
,则 ![]() ,
,
若 ![]() ,则
,则 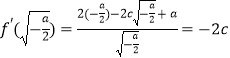 ,所以
,所以 ![]() ,
,
解得 ![]() ,不符合题意;
,不符合题意;
故 ![]() ,则
,则 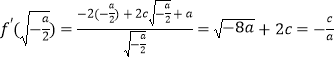 ,
,
整理得, ![]() ,由c>0得,
,由c>0得, ![]() ,
,
令 ![]() ,则
,则 ![]() ,t>2,所以
,t>2,所以 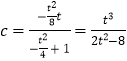 ,
,
设 ![]() ,则
,则 ![]() ,
,
当 ![]() 时,g′(t)<0,g(t)在
时,g′(t)<0,g(t)在 ![]() 上单调减;
上单调减;
当 ![]() 时,g′(t)>0,g(t)在
时,g′(t)>0,g(t)在 ![]() 上单调增.
上单调增.
所以,函数g(t)的最小值为 ![]() ,故实数c的最小值为
,故实数c的最小值为 ![]()
【解析】(1)求函数的导数,利用函数单调性和导数之间的关系,即可求f(x)的单调区间;(2)若f(x)≥ ![]() 对x∈(c,+∞)恒成立,则只需求出f(x)的最小值即可;(3)由l1⊥l2知,
对x∈(c,+∞)恒成立,则只需求出f(x)的最小值即可;(3)由l1⊥l2知, ![]() ,得到
,得到 ![]() ,分类讨论,再由导数与单调性的关系,即可得到实数c的最小值.
,分类讨论,再由导数与单调性的关系,即可得到实数c的最小值.
【考点精析】掌握利用导数研究函数的单调性和函数的极值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xsinx,有下列四个结论: ①函数f(x)的图象关于y轴对称;
②存在常数T>0,对任意的实数x,恒有f(x+T)=f(x);
③对于任意给定的正数M,都存在实数x0 , 使得|f(x0)|≥M;
④函数f(x)在[0,π]上的最大值是 ![]() .
.
其中正确结论的序号是(请把所有正确结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆心为
是圆心为![]() 的圆
的圆![]() 上的动点,点
上的动点,点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)矩形![]() 的边所在直线与曲线
的边所在直线与曲线![]() 均相切,设矩形
均相切,设矩形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E: ![]() (a>b>0),其长轴长是短轴长的
(a>b>0),其长轴长是短轴长的 ![]() 倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2
倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2 ![]() .
.
(1)求椭圆E的方程;
(2)设过右焦点F2且与x轴不垂直的直线l交椭圆E于P,Q两点,在线段OF2(O为坐标原点)上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设幂函数f(x)=(a﹣1)xk(a∈R,k∈Q)的图象过点 ![]() .
.
(1)求k,a的值;
(2)若函数h(x)=﹣f(x)+2b ![]() +1﹣b在[0,2]上的最大值为3,求实数b的值.
+1﹣b在[0,2]上的最大值为3,求实数b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是递增的等差数列,a1 , a2是方程x2﹣4x+3=0的两根.
(1)求数列{an}的通项公式;
(2)求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com