
【题目】已知函数![]() (
(![]() ,
,![]() )的图象与
)的图象与![]() 轴交点的横坐标构成一个公差为
轴交点的横坐标构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位,纵坐标扩大到原来的2倍得到函数
个单位,纵坐标扩大到原来的2倍得到函数![]() 的图象,则下列关于函数
的图象,则下列关于函数![]() 的命题中正确的是( )
的命题中正确的是( )
A.函数![]() 是奇函数B.
是奇函数B.![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C.![]() 在
在![]() 上是增函数D.当
上是增函数D.当![]() 时,函数
时,函数![]() 的值域是
的值域是![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为![]() ,墙
,墙![]() 的长度为
的长度为![]() 米,(已有两面墙的可利用长度足够大),记
米,(已有两面墙的可利用长度足够大),记![]() .
.
(1)若![]() ,求
,求![]() 的周长(结果精确到0.01米);
的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积,![]() 的面积尽可能大,当
的面积尽可能大,当![]() 为何值时,该活动室面积最大?并求出最大面积.
为何值时,该活动室面积最大?并求出最大面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在常数 k(k∈N * , k≥2)、d、t( d , t∈R),使得无穷数列 {a n }满足a n +1 ,则称数列{an }为“段差比数列”,其中常数 k、d、t 分别叫做段长、段差、段比.设数列 {bn }为“段差比数列”.
,则称数列{an }为“段差比数列”,其中常数 k、d、t 分别叫做段长、段差、段比.设数列 {bn }为“段差比数列”.
(1)已知 {bn }的首项、段长、段差、段比分别为1、 2 、 d 、 t .若 {bn }是等比数列,求 d 、 t 的值;
(2)已知 {bn }的首项、段长、段差、段比分别为1、3 、3 、1,其前 3n 项和为 S3n .若不等式 S3n≤ λ 3n1对 n ∈ N *恒成立,求实数 λ 的取值范围;
(3)是否存在首项为 b,段差为 d(d ≠ 0 )的“段差比数列” {bn },对任意正整数 n 都有 bn+6 = bn ,若存在, 写出所有满足条件的 {bn }的段长 k 和段比 t 组成的有序数组 (k, t );若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“
上的“![]() 类函数”,求是实数
类函数”,求是实数![]() 的最小值;
的最小值;
(3)若
![]() 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,若对于任意实数对
,若对于任意实数对![]() ,存在
,存在![]() ,使
,使![]() 成立,则称集合
成立,则称集合![]() 是“垂直对点集” .给出下列四个集合:
是“垂直对点集” .给出下列四个集合:
① ![]() ;
;
②![]() ;
;
③ ![]() ;
;
④![]() .
.
其中是“垂直对点集”的序号是( ).
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
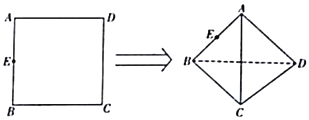
【题目】在正方形![]() 中,边长
中,边长![]() ,
,![]() 的中点为
的中点为![]() ,现将
,现将![]() 沿对角线
沿对角线![]() 翻折(如图),则在翻折的过程中.下列说法正确的是______.(填正确命题的序号)
翻折(如图),则在翻折的过程中.下列说法正确的是______.(填正确命题的序号)
①直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() (
(![]() ,
,![]() 不重合时);
不重合时);
②三棱锥![]() 体积的最大值为
体积的最大值为![]() ;
;
③三棱锥![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④点![]() 运动形成的轨迹为椭圆的一部分.
运动形成的轨迹为椭圆的一部分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数)上任意一点
为参数)上任意一点![]() 经过伸缩变换
经过伸缩变换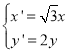 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com