
【题目】如图,在正三棱柱![]() (侧棱垂直于底面,且底面三角形
(侧棱垂直于底面,且底面三角形![]() 是等边三角形)中,
是等边三角形)中,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
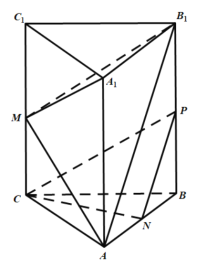
(1)求证:平面![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() 使
使![]() 平面
平面![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,也请说明理由.
的位置;若不存在,也请说明理由.
【答案】(1)证明见解析;(2)存在;点![]() 在
在![]() 处
处
【解析】
(1)要证明平面![]() ∥平面
∥平面![]() ,只需证明
,只需证明![]() ∥平面
∥平面![]() ,
,![]() ∥平面
∥平面![]() 即可;
即可;
(2)在线段![]() 上存在一点
上存在一点![]() ,它就是点
,它就是点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,只需证明
,只需证明![]() ,
,![]() ,再利用线面垂直的判定定理即可得到证明.
,再利用线面垂直的判定定理即可得到证明.
证明:(1)因为![]() 分别是
分别是![]() 的中点,
的中点,
所以![]() ∥
∥![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
因为![]() 分别是
分别是![]() 的中点,四边形
的中点,四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,且
,且![]() ∥
∥![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ∥
∥![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() ∥平面
∥平面![]() .
.
(2)在线段![]() 上存在一点
上存在一点![]() ,它就是点
,它就是点![]() ,使得
,使得![]() 平面
平面![]() .
.
连接![]() ,过点
,过点![]() 作
作![]() 垂直于
垂直于![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
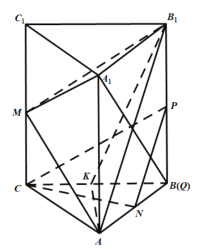
因为在正三棱柱![]() 中,
中,![]() ,底面三角形
,底面三角形![]() 是等边三角形,
是等边三角形,
所以四边形![]() 是正方形,
是正方形,
所以![]() .
.
易证![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,三棱柱
,三棱柱![]() 为直三棱柱,
为直三棱柱,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的棱长均为6,其内有
的棱长均为6,其内有![]() 个小球,球
个小球,球![]() 与三棱锥
与三棱锥![]() 的四个面都相切,球
的四个面都相切,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切,如此类推,…,球
都相切,如此类推,…,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),则球
),则球![]() 的体积等于__________,球
的体积等于__________,球![]() 的表面积等于__________.
的表面积等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东京夏季奥运会推迟至2021年7月23日至8月8日举行,此次奥运会将设置4![]() 100米男女混泳接力赛这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳
100米男女混泳接力赛这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员参加比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者蛙泳,剩下2名运动员四种泳姿都可以承担,则中国队参赛的安排共有( )
自由泳的接力顺序,每种泳姿100米且由1名运动员完成,且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或者蛙泳,剩下2名运动员四种泳姿都可以承担,则中国队参赛的安排共有( )
A.144种B.8种C.24种D.12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X是有限集,t为正整数,F是包含t个子集的子集族:F=![]() .如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,
.如果F中的部分子集构成的集族S满足:对S中任意两个不相等的集合A、B,![]() 均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足
均不成立,则称S为反链.设S1为包含集合最多的反链,S2是任意反链.证明:存在S2到S1的单射f,满足![]() 或
或![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈(![]() ,
,![]() ),则输入的n的值为( )
),则输入的n的值为( )
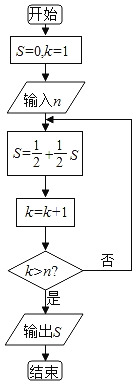
A.7B.6C.5D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() (a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为
(a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为![]() ,离心率为
,离心率为![]() .
.

(1)求椭圆的标准方程;
(2)当直线MN的斜率为![]() 时,求
时,求![]() 的值;
的值;
(3)若以MN为直径的圆与x轴相交的右交点为P(t,0),求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com