
分析 (1)由已知条件利用十位和百位作茎,利用个位作叶,能作出茎叶图.
(2)由已知条件能求出该组数据的平均值、方差、标准差.
(3)通过观察茎叶图得出对品种A与B的亩产量极其稳定性进行比较.
解答 解:(1)由已知条件作出茎叶图,如下: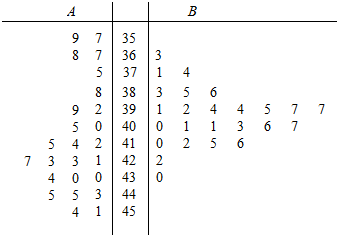
(2)该组数据的平均值:$\overline{x}$=$\frac{359+367+400+388+434+392}{6}$=390.
该组数据的方差:S2=$\frac{1}{6}$[(359-390)2+(367-390)2+(400-390)2+(388-390)2+(434-390)2+(392-390)2]=3534,
该组数据的标准差:S=$\sqrt{3534}$.
(3)通过观察茎叶图得出:
①品种A的亩产平均数(或均值)比品种B高.
②品种A的亩产标准准差(或方差)比品种B大,故品种A的亩产稳定性较差.
点评 本题考查茎叶图及该组数据的平均值、方差、标准差的求法,通过观察茎叶图,对品种A与B的亩产量极其稳定性进行比较,是基础题,注意茎叶图的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈N+,2x<2 | B. | ?x∉N+,2x<2 | C. | ?x∉N+,2x<2 | D. | ?x∈N+,2x<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 算法需要一步步执行,且每一步都能得到唯一的结果 | |
| B. | 算法的一个共同特点是对一类问题都有效而不是个别问题 | |
| C. | 任何问题都可以用算法来解决 | |
| D. | 算法一般是机械的,有时要进行大量重复的计算,它的优点是一种通法 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com