练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
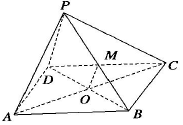
    4．如图，P为矩形ABCD所在平面外一点，矩形对角线交点为O，M为PB的中点，给出下面四个命题：①OM∥面PCD；②OM∥面PBC；③OM∥面PDA；④OM∥面PBA．其中正确命题的个数是（　　）
    A．1B．2C．3D．4

    分析 在①中，由OM∥PD，得到OM∥面PCD；在②中，OM∩平面PBC=M；在③中，由OM∥PD，得OM∥面PCD；在④中，OM∩平面PBA=M．

    解答 解：由P为矩形ABCD所在平面外一点，矩形对角线交点为O，M为PB的中点，知：
    在①中，∵矩形ABCD中，O是BD中点，M为PB的中点，
    ∴OM∥PD，又OM?平面PCD，PD?平面PCD，∴OM∥面PCD，故①正确；
    在②中，∵OM∩平面PBC=M，∴OM∥面PBC不成立，故②错误；
    在③中，∵矩形ABCD中，O是BD中点，M为PB的中点，
    ∴OM∥PD，又OM?平面PDA，PD?平面PDA，∴OM∥面PCD，故③正确；
    在④中，∵OM∩平面PBA=M，∴OM∥面PBA不成立，故④错误．
    故选：B．

    点评 本题考查命题真判断，是中档题，解题时要认真审题，注意空间思维能力的培养．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

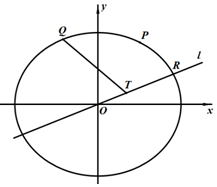    10．如图，在平面直角坐标系xOy中，点$P（1，\frac{3}{2}）$和动点Q（m，n）都在离心率为$\frac{1}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）上，其中m＜0，n＞0．
    （1）求椭圆的方程；
    （2）若直线l的方程为3mx+4ny=0，点R（点R在第一象限）为直线l与椭圆的一个交点，点T在线段OR上，且QT=2．
    ①若m=-1，求点T的坐标；
    ②求证：直线QT过定点S，并求出定点S的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．定义在实数集R上的函数f（x）都可以写为一个奇函数g（x）与一个偶函数h（x）之和的形式，如果f（x）=2x+1，那么（　　）
    A．$g（x）=\frac{{{2^x}-{2^{-x}}}}{2}$，$h（x）=\frac{{{2^x}+{2^{-x}}}}{2}$B．$g（x）=\frac{{{2^x}-{2^{-x}}}}{2}$，$h（x）=1+\frac{{{2^x}+{2^{-x}}}}{2}$
    C．$g（x）=1+\frac{{{2^x}-{2^{-x}}}}{2}$，$h（x）=\frac{{{2^x}+{2^{-x}}}}{2}$D．$g（x）=\frac{{{2^x}-{2^{-x}}+1}}{2}$，$h（x）=\frac{{{2^x}+{2^{-x}}+1}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520名女性中有6人患色盲．
    （1）根据以上数据建立一个2×2列联表；
    （2）若认为“性别与患色盲有关系”，则出错的概率会是多少？
    附1：随机变量：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（c+a）（b+d）}$
    附2：临界值参考表：
    P（K2≥x0）0.100.050.0250.100.0050.001
    x02.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．方程$\frac{x|x|}{16}+\frac{y|y|}{9}=-1$的曲线即为函数y=f（x）的图象，对于函数y=f（x），有如下结论：
    ①f（x）在R上单调递减；
    ②函数F（x）=4f（x）+3x不存在零点；
    ③y=f（|x|）的最大值为3；
    ④若函数g（x）和f（x）的图象关于原点对称，则y=g（x）由方程$\frac{y|y|}{16}+\frac{x|x|}{9}=1$确定．
    其中所有正确的命题序号是（　　）
    A．③④B．②③C．①④D．①②

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知log23=a，log72=b，则log421=$\frac{ab+1}{2b}$．（用a，b表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=2sin（$\frac{1}{3}x-\frac{π}{6}$）．
    （1）用“五点法”画出函数在一个周期内的图象；
    （2）完整叙述函数f（x）=2sin（$\frac{1}{3}x-\frac{π}{6}$）的图象可以由函数f（x）=2sinx的图象经过两步怎样的变换得到；
    （3）求使f（x）≥0成立的取值集合．
    解：（1）
    $\frac{1}{3}$x-$\frac{π}{6}$0$\frac{π}{2}$π$\frac{3π}{2}$2
    x$\frac{π}{2}$2π$\frac{7π}{2}$5π$\frac{13π}{2}$
    y02020

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．记关于x的不等于$\frac{x-3}{x+1}≤0$的解集为P，不等式|x-a|≤1的解集为Q．
    （1）求出集合P；
    （2）若P∩Q=Q，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．某企业生产A、B、C三种家电，经市场调查决定调整生产方案，计划本季度（按不超过480个工时计算）生产A、B、C三种家电共120台，其中A家电至少生产20台，已知生产A、B、C三种家电每台所需的工时分别为3、4、6个工时，每台的产值分别为20、30、40千元，则按此方案生产，此季度最高产值为（　　）千元．
    A．3600B．350C．4800D．480

    查看答案和解析>>

    同步练习册答案