
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在椭圆
在椭圆![]() :
:![]() 上,该椭圆的左顶点
上,该椭圆的左顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 外一点
外一点![]() 满足,
满足,![]() 平行于
平行于![]() 轴,
轴,![]() ,动点
,动点![]() 在直线
在直线![]() 上,满足
上,满足![]() .设过点
.设过点![]() 且垂直
且垂直![]() 的直线
的直线![]() ,试问直线
,试问直线![]() 是否过定点?若过定点,请写出该定点,若不过定点请说明理由.
是否过定点?若过定点,请写出该定点,若不过定点请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据点到直线的距离公式可求出a的值,即可得椭圆方程;
(2)由题意M(x0,y0),N(x0,y1),P(2![]() ,t),根据
,t),根据![]() ,可得y1=2y0,由
,可得y1=2y0,由![]() ,可得2
,可得2![]() x0+2y0t=6,再根据向量的运算可得
x0+2y0t=6,再根据向量的运算可得![]() ,即可证明.
,即可证明.
(1)左顶点A的坐标为(﹣a,0),∵![]() =
=![]() ,∴|a﹣5|=3,解得a=2或a=8(舍去),∴椭圆C的标准方程为
,∴|a﹣5|=3,解得a=2或a=8(舍去),∴椭圆C的标准方程为![]() +y2=1,
+y2=1,
(2)由题意M(x0,y0),N(x0,y1),P(2![]() ,t),则依题意可知y1≠y0,
,t),则依题意可知y1≠y0,![]() 得(x0﹣2 x0,y1﹣2y0)
得(x0﹣2 x0,y1﹣2y0)![]() (0,y1﹣y0)=0,整理可得y1=2y0,或y1=y0 (舍),
(0,y1﹣y0)=0,整理可得y1=2y0,或y1=y0 (舍),![]() ,得(x0,2y0)(2
,得(x0,2y0)(2![]() ﹣x0,t﹣2y0)=2,整理可得2
﹣x0,t﹣2y0)=2,整理可得2![]() x0+2y0t=x02+4y02+2=6,由(1)可得F(
x0+2y0t=x02+4y02+2=6,由(1)可得F(![]() ,0),∴
,0),∴![]() =(
=(![]() ﹣x0,﹣2y0),∴
﹣x0,﹣2y0),∴![]()
![]() =(
=(![]() ﹣x0,﹣2y0)(2
﹣x0,﹣2y0)(2![]() ,t)=6﹣2
,t)=6﹣2![]() x0﹣2y0t=0,∴NF⊥OP,故过点N且垂直于OP的直线过椭圆C的右焦点F.
x0﹣2y0t=0,∴NF⊥OP,故过点N且垂直于OP的直线过椭圆C的右焦点F.


科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两个不同的平面,则
是两个不同的平面,则![]() 的必要不充分条件是( )
的必要不充分条件是( )
A.![]() 内存在一条直线垂直于
内存在一条直线垂直于![]() 内的两条相交直线
内的两条相交直线
B.平行于![]() 的一个平面与
的一个平面与![]() 垂直
垂直
C.![]() 内存在一条直线垂直于
内存在一条直线垂直于![]() 内的无数条直线
内的无数条直线
D.垂直于![]() 的一条直线与
的一条直线与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装公司,为确定明年![]() 类服装的广告费用,对往年广告费
类服装的广告费用,对往年广告费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:件)和年利润
(单位:件)和年利润![]() (单位:千元)的影响.对2011-2018广告费
(单位:千元)的影响.对2011-2018广告费![]() 和年销售量
和年销售量![]() 数据进行了处理,分析出以下散点图和统计量:
数据进行了处理,分析出以下散点图和统计量:

|
|
|
|
|
|
|
45 | 580 | 2025 | 297 | 1600 | 960 | 1440 |
表中![]()
(1)由散点图可知,![]() 和
和![]() 更适合作为年销售量
更适合作为年销售量![]() 关于年广告费
关于年广告费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果和表中数据求![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)已知该类服装年利率![]() 与
与![]() 的关系为
的关系为![]() .由(2)回答以下问题:年广告费用
.由(2)回答以下问题:年广告费用![]() 等于60时,年销售量及年利润的预报值为多少?年广告费用为何值时,年利率的预报值最小?
等于60时,年销售量及年利润的预报值为多少?年广告费用为何值时,年利率的预报值最小?
对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设L、M、N分别为![]() 的∠BAC、∠ CBA、∠ ACB内的点,且∠BAL=∠ ACL,∠ LBA=∠ LAC,∠ CBM=∠ BAM,∠ MCB=∠ MBA,∠ ACN=∠ CBN,∠ NAC=∠ NCB.
的∠BAC、∠ CBA、∠ ACB内的点,且∠BAL=∠ ACL,∠ LBA=∠ LAC,∠ CBM=∠ BAM,∠ MCB=∠ MBA,∠ ACN=∠ CBN,∠ NAC=∠ NCB.
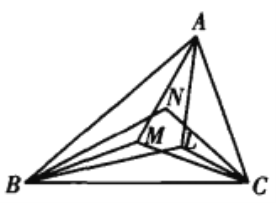
证明:(1) AL、BM、CN三线交于一点P;
(2)L、M、N、P四点共圆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: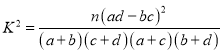 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象上所有点的横坐标缩小到原来的
的图象上所有点的横坐标缩小到原来的![]() 倍(纵坐标不变),再把得到图象上所有点向右平移
倍(纵坐标不变),再把得到图象上所有点向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象.则下列命题正确的是( )
的图象.则下列命题正确的是( )
A.函数![]() 在区间
在区间![]() ,
,![]() 上单调递减
上单调递减
B.函数![]() 在区间
在区间![]() ,
,![]() 上单调递增
上单调递增
C.函数![]() 的图象关于直线
的图象关于直线![]() ,
,![]() 对称
对称
D.函数![]() 的图象关于点
的图象关于点![]() ,
,![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,以便利润最大化,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,以便利润最大化,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该店这款新面包每日出炉数设定为![]() 个
个
(i)求日需求量为![]() 个时的当日利润;
个时的当日利润;
(ii)求这![]() 天的日均利润.
天的日均利润.
相关公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·重庆高二检测)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.
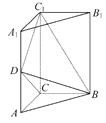
(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com