
【题目】曲线C的参数方程为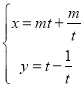 (
(![]() 为参数,
为参数,![]() ),以原点为极点,x轴正半轴为极轴建立极坐标系,直线
),以原点为极点,x轴正半轴为极轴建立极坐标系,直线![]() 与直线
与直线![]() 交于点P,动点Q在射线OP上,且满足|OQ||OP|=8.
交于点P,动点Q在射线OP上,且满足|OQ||OP|=8.
(1)求曲线C的普通方程及动点Q的轨迹E的极坐标方程;
(2)曲线E与曲线C的一条渐近线交于P1,P2两点,且|P1P2|=2,求m的值.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为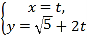 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),以坐标原点
是参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 取最大值时
取最大值时![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=3,且对任意的正整数n,都有an+1=λan+2×3n,其中常数λ>0.
(1)设bn![]() .当λ=3时,求数列{bn}的通项公式;
.当λ=3时,求数列{bn}的通项公式;
(2)若λ≠1且λ≠3,设cn=an![]() ,证明:数列{cn}为等比数列;
,证明:数列{cn}为等比数列;
(3)当λ=4时,对任意的n∈N*,都有an≥M,求实数M的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来就一直使用的纪年方法.其中干支是天干:甲、乙、丙、丁、戊、已、庚、辛、壬、癸十个符号;地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个符号.把干支顺序相配正好六十为一周,周而复始,循环记录,即甲子、乙丑、丙寅、…….2020年是“庚子年”,则我国建国一百周年(2049年)是_______年.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C1的参数方程为![]() (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为![]() ,曲线C3的极坐标方程为
,曲线C3的极坐标方程为![]() .
.
(1)把曲线C1的参数方程化为极坐标方程;
(2)曲线C3与曲线C1交于O,A,与曲线C2交于O,B,求|AB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com