
 =(1,1),
=(1,1), =(1,0),
=(1,0), 满足
满足 =0,且
=0,且 =
=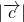 ,
,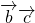 >0
>0 ;
;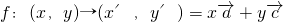
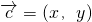 ,则
,则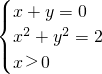
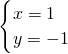
 =(1,-1)
=(1,-1)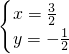
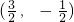
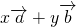 =(x+y,x-y)
=(x+y,x-y)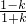 =k,
=k,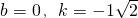 ,
,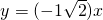 .
.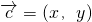 ,由已知得到关于x、y的方程组,求出x、y,即求得向量
,由已知得到关于x、y的方程组,求出x、y,即求得向量 ;
;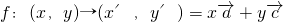 ,①求映射f下(1,2)原象,列出方程,解方程即可;②存在性命题的探讨,转化为(1+k)y=(1-k)x-b与y=kx+b表示同一直线,对应系数相等,求得直线方程.
,①求映射f下(1,2)原象,列出方程,解方程即可;②存在性命题的探讨,转化为(1+k)y=(1-k)x-b与y=kx+b表示同一直线,对应系数相等,求得直线方程.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
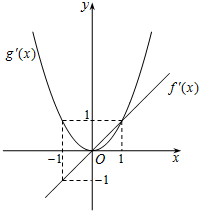 (2013•武汉模拟)已知函数f'(x)、g'(x)分别是二次函数f(x)和三次函数g(x)的导函数,它们在同一坐标系下的图象如图所示:
(2013•武汉模拟)已知函数f'(x)、g'(x)分别是二次函数f(x)和三次函数g(x)的导函数,它们在同一坐标系下的图象如图所示:查看答案和解析>>
科目:高中数学 来源:2014届广东省高一期中考试文科数学试卷A卷(解析版) 题型:解答题
已知函数f(x)(x∈R)满足f(x)= ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1= ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)= ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)= .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
= =
= =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1= ,∴b1=
,∴b1= -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn= +
+ +…+
+…+ <
< +
+ +…+
+…+
= =1-
=1- <1(n∈N*).
<1(n∈N*).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省景德镇市高三(上)11月月考数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省景德镇市高三(上)第一次质检数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com