
 中,
中, ,
,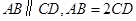 ,
, 分别为
分别为 的中点.
的中点.
 ;
; .
.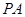 的中点
的中点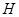 ,连接
,连接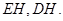
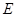 为
为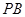 的中点,所以
的中点,所以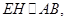
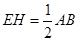 ,
,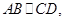
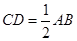 ,
,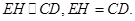
 是平行四边形.
是平行四边形.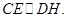
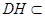 平面
平面 ,
,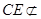 平面
平面 ,
,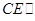 平面
平面 .
.
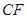 .
.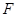 为
为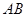 的中点,所以
的中点,所以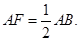
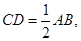 所以
所以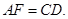
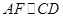 ,所以四边形
,所以四边形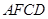 为平行四边形,因此
为平行四边形,因此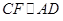 .
.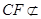 平面
平面 ,所以
,所以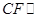 平面
平面 .
.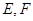 分别为
分别为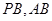 的中点,所以
的中点,所以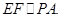
 平面
平面 ,所以
,所以 平面
平面 .
.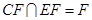 ,所以平面
,所以平面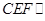 平面
平面 .
.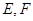 分别为
分别为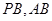 的中点,
的中点,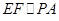 ,又因为
,又因为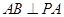 ,所以
,所以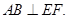
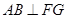 .
.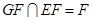 ,
,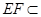 平面
平面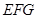 ,
,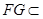 平面
平面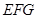 ,
,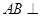 平面
平面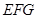 .
.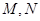 分别为
分别为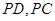 的中点,所以
的中点,所以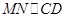 .
.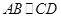 ,所以
,所以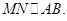
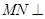 平面
平面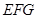 ,
,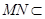 平面
平面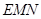 ,所以平面
,所以平面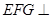 平面
平面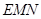 .
.
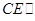 平面
平面 ,可证明平面
,可证明平面 与
与 所在的某个平面平行,不难发现平面
所在的某个平面平行,不难发现平面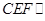 平面
平面 .证明平面
.证明平面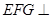 平面
平面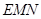 时,可选择一个平面内的一条直线(
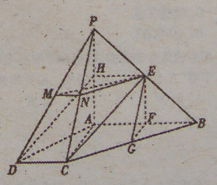
时,可选择一个平面内的一条直线(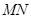 )与另一个平面垂直.线面关系与面面关系的判断离不开判定定理和性质定理,而形成结论的“证据链”依然是通过挖掘题目已知条件来实现的,如图形固有的位置关系,中点形成的三角形的中位线等,都为论证提供了丰富的素材.
)与另一个平面垂直.线面关系与面面关系的判断离不开判定定理和性质定理,而形成结论的“证据链”依然是通过挖掘题目已知条件来实现的,如图形固有的位置关系,中点形成的三角形的中位线等,都为论证提供了丰富的素材.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:不详 题型:解答题
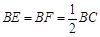 ,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点
,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点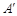 ,连结A¢B.
,连结A¢B.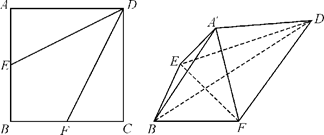
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
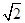 ,则 M 到面 ABC 的距离为( )
,则 M 到面 ABC 的距离为( )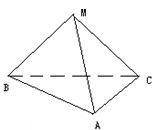
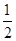
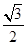
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中(图1),
中(图1), ,
,
 中点为
中点为 ,将图1沿直线
,将图1沿直线 折起,使二面角
折起,使二面角 为
为 (图2)
(图2)

 作直线
作直线 平面
平面 ,且
,且 平面
平面 =
= ,求
,求 的长度。
的长度。 与平面
与平面 所成角的正弦值。
所成角的正弦值。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com