
【题目】已知椭圆C1与双曲线C2有相同的左右焦点F1,F2,P为椭圆C1与双曲线C2在第一象限内的一个公共点,设椭圆C1与双曲线C2的离心率分别为e1,e2,且![]() =
=![]() ,若∠F1PF2=
,若∠F1PF2=![]() ,则双曲线C2的渐近线方程为( )
,则双曲线C2的渐近线方程为( )
A. x±y=0 B. x±![]() y=0
y=0
C. x±![]() y=0 D. x±2y=0
y=0 D. x±2y=0
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在一次“汉马”(武汉马拉松比赛的简称)全程比赛中,50名参赛选手(24名男选手和26名女选手)的成绩(单位:分钟)分别为数据![]() (成绩不为0).
(成绩不为0).
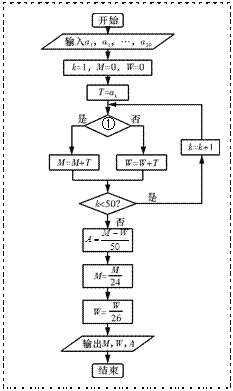
(Ⅰ)24名男选手成绩的茎叶图如图⑴所示,若将男选手成绩由好到差编为1~24号,再用系统抽样方法从中抽取6人,求其中成绩在区间![]() 上的选手人数;
上的选手人数;

(Ⅱ)如图⑵所示的程序用来对这50名选手的成绩进行统计.为了便于区别性别,输入时,男选手的成绩数据用正数,女选手的成绩数据用其相反数(负数),请完成图⑵中空白的判断框①处的填写,并说明输出数值![]() 和
和![]() 的统计意义.
的统计意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325 8430 8215 7453 7446 6754
7638 6834 6460 6830 9860 8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为![]() )
)
组别 | 步数分组 | 频数 |
|
| 2 |
|
| 10 |
|
|
|
|
| 2 |
|
|
|
(Ⅰ)写出![]() 的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
(Ⅱ)记![]() 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为![]() ,
,![]() ,
,![]() 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为![]() ,
,![]() ,试分别比较
,试分别比较![]() 与以
与以![]() ,
,![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从上述![]() 两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为
两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B两地相距24km.甲车、乙车先后从A地出发匀速驶向B地.甲车从A地到B地需行驶25min;乙车从A地到B地需行驶20min.乙车比甲车晚出发2min.
(1)分别写出甲、乙两车所行路程关于甲车行驶时间的函数关系式;
(2)甲、乙两车何时在途中相遇?相遇时距A地多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数![]() 的一条对称轴是
的一条对称轴是![]() ;
;
②函数![]() 的图象关于点(
的图象关于点(![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数
④若![]() ,则
,则![]() ,其中
,其中![]()
以上四个命题中正确的有 (填写正确命题前面的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=8x,圆M:(x-2)2+y2=4,点N为抛物线E上的动点,O为坐标原点,线段ON的中点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)点Q(x0,y0)(x0≥5)是曲线C上的点,过点Q作圆M的两条切线,分别与x轴交于A,B两点,求△QAB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况.发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)试估计该市市民正确书写汉字的个数的平均数与中位数;
(2)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com