
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,证明:
,证明:![]() 成等差数列;
成等差数列;
(3)若函数![]() 有三个零点
有三个零点![]() ,对任意的
,对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)由导数的几何意义可得解;
(2)由等差数列的判定,只需证明![]() ,代入运算即可;
,代入运算即可;
(3)由导数的综合应用,求函数的单调性,再求函数的最值,解不等式即可得解.
解:(1)由函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
得![]() ,又
,又![]() ,
,
即![]() ,
,
故![]() ;
;
(2)要证![]() 成等差数列,
成等差数列,
只需证明![]() ,
,
又函数![]() 有两个极值点
有两个极值点![]() ,则
,则![]() ,
,
![]() +
+![]() =
=
=![]() ,
,
命题得证;
(3)由函数![]() 有三个零点
有三个零点![]() ,
,
得![]() ,解得
,解得![]() 且
且![]() 有两个根为
有两个根为![]() ,
,
于是有![]() ,即
,即![]() ,
,
![]() 有两个相异的实根,不妨设为
有两个相异的实根,不妨设为![]() ,
,
①当![]() 时,
时,![]() ,
,
函数在![]() 为减函数,在
为减函数,在![]() 为增函数,
为增函数,
又![]()
所以![]() ,
,
故不等式![]() 恒成立,
恒成立,
② 当![]() 时,
时,![]() ,
,
函数![]() 在
在![]() 为减函数,在
为减函数,在![]() ,
, ![]() 为增函数,
为增函数,
由![]() ,
,![]()
故![]() =
=![]() ,
,
对于任意的![]() ,不等式
,不等式![]() 恒成立,
恒成立,
于是![]()
![]() ,
,
又![]() ,
,
故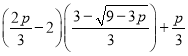
![]() ,
,
令![]()
![]()
,则![]() ,
,
解得![]() ,
,
解得![]() ,即
,即![]() ,
,
即![]()
综上可得![]() 的取值范围为
的取值范围为![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为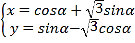 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种规格的矩形瓷砖![]() 根据长期检测结果,各厂生产的每片瓷砖质量
根据长期检测结果,各厂生产的每片瓷砖质量![]() 都服从正态分布
都服从正态分布![]() ,并把质量在
,并把质量在![]() 之外的瓷砖作为废品直接回炉处理,剩下的称为正品.
之外的瓷砖作为废品直接回炉处理,剩下的称为正品.
(Ⅰ)从甲陶瓷厂生产的该规格瓷砖中抽取10片进行检查,求至少有1片是废品的概率;
(Ⅱ)若规定该规格的每片正品瓷砖的“尺寸误差”计算方式为:设矩形瓷砖的长与宽分别为![]() 、
、![]() ,则“尺寸误差”
,则“尺寸误差”![]() 为
为![]() ,按行业生产标准,其中“优等”、“一级”、“合格”瓷砖的“尺寸误差”范围分别是
,按行业生产标准,其中“优等”、“一级”、“合格”瓷砖的“尺寸误差”范围分别是![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() (正品瓷砖中没有“尺寸误差”大于
(正品瓷砖中没有“尺寸误差”大于![]() 的瓷砖),每片价格分别为7.5元、6.5元、5.0元.现分别从甲、乙两厂生产的该规格的正品瓷砖中随机抽取100片瓷砖,相应的“尺寸误差”组成的样本数据如下:
的瓷砖),每片价格分别为7.5元、6.5元、5.0元.现分别从甲、乙两厂生产的该规格的正品瓷砖中随机抽取100片瓷砖,相应的“尺寸误差”组成的样本数据如下:
尺寸误差 | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
频数 | 10 | 30 | 30 | 5 | 10 | 5 | 10 |
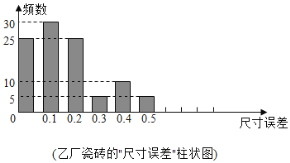
(甲厂瓷砖的“尺寸误差”频数表)用这个样本的频率分布估计总体分布,将频率视为概率.
(ⅰ)记甲厂该种规格的2片正品瓷砖卖出的钱数为![]() (元
(元![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
(ⅱ)由如图可知,乙厂生产的该规格的正品瓷砖只有“优等”、“一级”两种,求5片该规格的正品瓷砖卖出的钱数不少于36元的概率.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ;
;![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
(1)若P是线段A1B的中点,求直线MP与直线AC所成角的大小;
(2)若![]() 是
是![]() 的中点,直线
的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段BP的长度.
,求线段BP的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年春晚都是万众瞩目的时刻,这些节目体现的文化内涵、历史背景等反映了社会的进步.国家的富强,人民生活水平的提高等.某学校高三年级主任开学初为了解学生在看春晚后对节目体现的文化内涵、历史背景等是否会在今年的高考题中体现进行过思考,特地随机抽取100名高三学生(其中文科学生50,理科学生50名),进行了调查.统计数据如表所示(不完整):
“思考过” | “没有思考过” | 总计 | |
文科学生 | 40 | 10 | |
理科学生 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有![]() 的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
(2)①现从上表的”思考过”的文理科学生中按分层抽样选出7人.再从这7人中随机抽取4人,记这4人中“文科学生”的人数为![]() ,试求
,试求![]() 的分布列与数学期望;
的分布列与数学期望;
②现设计一份试卷(题目知识点来自春晚相关知识整合与变化),假设“思考过”的学生及格率为![]() ,“没有思考过”的学生的及格率为
,“没有思考过”的学生的及格率为![]() .现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
.现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
附参考公式: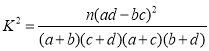 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com