
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
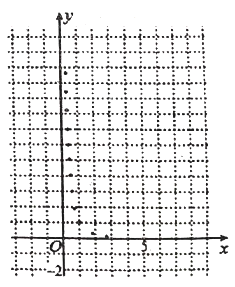
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为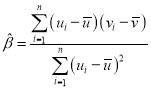 ,
,![]()
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是圆柱![]() 的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,
的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,![]()
![]()
![]() :
:
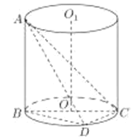
(1)求直线AC与平面ABD所成角的大小;
(2)求点B到平面ACD的距离;
(3)将四面体ABCD绕母线AB旋转一周,求由![]() 旋转而成的封闭几何体的体积;
旋转而成的封闭几何体的体积;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 焦点F,过点F且斜率为2的直线与抛物线交于A、B两点,且
焦点F,过点F且斜率为2的直线与抛物线交于A、B两点,且![]() .
.
(1)求抛物线E的方程;
(2)设O是坐标原点,P,Q是抛物线E上分别位于x轴两侧的两个动点,且![]()
①证明:直线PQ必过定点,并求出定点G的坐标;
②过G作PQ的垂线交抛物线于C,D两点,求四边形PCQD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—5:参数方程选讲]
在直角坐标系xoy中,曲线![]() 的参数方程是
的参数方程是 (t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
(t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两曲线交点为A、B,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】郑汴一体化是依托郑州省会城市资源优势发展开封的省级战略,实施至今,取得了一系列的成就:两城电信同价,金融同城,郑开大道全线贯通,城际列车实常态化运营.随着郑汴一体化的深入推进,很多人认为郑州开封未来有望合并.为了解市民对郑汴合并的态度,现随机抽查55人,结果按年龄分类统计形成如下表格:
支持 | 反对 | 合计 | |
不足35岁 | 20 | ||
35岁以上 | 30 | ||
合计 | 25 | 55 |
(1)请完成上面的2×2列联表,并判断是否有99.5%的把握认为市民对郑汴合并的态度与年龄有关?
(2)在上述样木中用分层抽样的方法,从攴持郑汴合并的两组市民中随机抽取6人作进一步调查,从这6人中任选2人,求恰有1位“不足35岁”的市民和1位“35岁及以上”的市民的概率.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.814 | 5.024 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com