
命题:“若空间两条直线a,b分别垂直平面α,则a∥b”,学生小夏这样证明:
设a,b与平面α分别相交于A,B,连接AB,
∵a⊥α,b⊥α,AB?α,①
∴a⊥AB,b⊥AB,②
∴a∥b.③
这里的证明有两个推理,即:
①⇒②和②⇒③,老师认为小夏的推理证明不正确,这两个推理中不正确的是 .
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:填空题
如图,PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上的一点,E、F分别是点A在PB、PC上的射影.给出下列结论: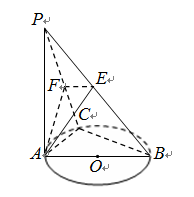
①AF⊥PB; ②EF⊥PB;
③AF⊥BC; ④AE⊥平面PBC.
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 是两个不同的平面,
是两个不同的平面, 是平面
是平面 及
及 之外的两条不同直线,给出四个论断:
之外的两条不同直线,给出四个论断:
① ②
② ③
③ ④
④ 。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知下列命题:
①设m为直线, 为平面,且m
为平面,且m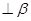 ,则“m//
,则“m// ”是“
”是“ ”的充要条件;
”的充要条件;
② 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;
③设随机变量 ~N(0,1),若P(
~N(0,1),若P( ≥2)=p,则P(-2<
≥2)=p,则P(-2< <0)=
<0)= ;
;
④若不等式|x+3|+|x-2|≥2m+1恒成立,则m的取值范围是( ,2);
,2);
⑤已知奇函数 满足
满足 ,且0<x<
,且0<x<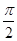 时
时 ,则函数
,则函数 在[
在[ ,
, ]上有5个零点.
]上有5个零点.
其中真命题的序号是 (写出全部真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知矩形ABCD,AB=1,BC= ,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,下列说法正确的是________.(填序号)
,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,下列说法正确的是________.(填序号)
①存在某个位置,使得直线AC与直线BD垂直;
②存在某个位置,使得直线AB与直线CD垂直;
③存在某个位置,使得直线AD与直线BC垂直;
④对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知四棱锥PABCD的顶点P在底面的射影恰好是底面菱形ABCD的两条对角线的交点,若AB=3,PB=4,则PA长度的取值范围为________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设a,b为空间的两条直线,α,β为空间的两个平面,给出下列命题:
①若a∥α,a∥β,则α∥β;②若a⊥α,α⊥β,则α⊥β;
③若a∥α,b∥α,则a∥b; ④若a⊥α,b⊥α,则a∥b.
上述命题中,所有真命题的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com