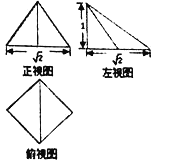
【题目】刘徽《九章算术商功》中将底面为长方形，两个三角面与底面垂直的四棱锥体叫做阳马．如图，是一个阳马的三视图，则其外接球的体积为（ ）
A.
B.
C.
D.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
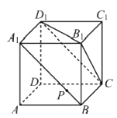
【题目】如图，在正方体
中，点
在线段
上移动，有下列判断：①平面
平面
；②平面
平面；③三棱锥
的体积不变；④
平面．其中，正确的是______．（把所有正确的判断的序号都填上）
查看答案和解析>>
科目：高中数学 来源： 题型：
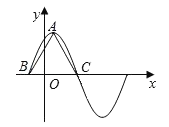
【题目】函数f（x）＝6cos2
sinωx﹣3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B，C为图象与x轴的交点，且△ABC为正三角形
（1）求ω的值及函数f（x）的表达式；
（2）若f（x0）
，且x0∈（
），求f（x0+1）的值
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合
是由数列
组成的集合，其中数列同时满足以下三个条件：
①数列共有
项，
；②
；③
（1）若等比数列
，求等比数列
的首项、公比和项数；
（2）若等差数列
是递增数列，并且
，常数
，求该数列的通项公式；
（3）若数列
，常数
，
，求证：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
，
是它的上顶点，点
各不相同且均在椭圆上.
（1）若
恰为椭圆长轴的两个端点，求
的面积；
（2）若
，求证：直线
过一定点；
（3）若
，
的外接圆半径为
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为
配方和
配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方的频数分布表:
指标值分组 | [90,94） | [94,98） | [98,102） | [102,106） | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
配方的频数分布表:
指标值分组 | [90,94） | [94,98） | [98,102） | [102,106] | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
（1）分别估计用
配方、配方生产的产品的优质品率;
（2）已知用配方生产的一件产品的利润(单位:元)与其质量指标值
的关系为
,估计用配方生产的一件产品的利润大于
的概率,并求用配方生产的上述
件产品的平均利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
