
【题目】已知O点为坐标原点,且点A(1,0),B(0,1),C(2sinθ,cosθ)
(1)若 ![]() ,求tanθ的值;
,求tanθ的值;
(2)若 ![]() =1,求sinθcosθ的值.
=1,求sinθcosθ的值.
【答案】
(1)解:∵A(1,0),B(0,1),C(2sinθ,cosθ),
∴ ![]() =(2sinθ﹣1,cosθ),
=(2sinθ﹣1,cosθ), ![]() =(2sinθ,cosθ﹣1),
=(2sinθ,cosθ﹣1),
∵ ![]() ,
,
∴(2sinθ﹣1)2+cos2θ=4sin2θ+(cosθ﹣1)2,
∴化为2sinθ=cosθ,
∴tanθ= ![]()
(2)解:∵ ![]() =(1,0)+2(0,1)=(1,2),
=(1,0)+2(0,1)=(1,2),
∵ ![]() =1,
=1,
∴2sinθ+2cosθ=1,
∴sinθ+cosθ= ![]() ,
,
∴sin2θ+cos2θ+2sinθcosθ= ![]() ,
,
∴sinθcosθ= ![]()
【解析】(1)利用向量的坐标运算、数量积的运算性质即可得出;(2)由数量积的坐标运算可得sinθ+cosθ= ![]() ,与sin2θ+cos2θ=1联立即可解出.
,与sin2θ+cos2θ=1联立即可解出.


科目:高中数学 来源: 题型:
【题目】已知点列An(xn , 0),n∈N* , 其中x1=0,x2=1.A3是线段A1A2的中点,A4是线段A2A3的中点,…,An+2是线段AnAn+1的中点,…设an=xn+1﹣xn . (Ⅰ)写出xn与xn﹣1、xn﹣2(n≥3)之间的关系式并计算a1 , a2 , a3;
(Ⅱ)猜想数列{an}的通项公式,并用数学归纳法加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=﹣tan2x,有下列说法: ①f(x)的定义域是{x∈R|x≠ ![]() +kπ,k∈Z}②f(x)是奇函数 ③在定义域上是增函数 ④在每一个区间(﹣
+kπ,k∈Z}②f(x)是奇函数 ③在定义域上是增函数 ④在每一个区间(﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() )(k∈Z)上是减函数 ⑤最小正周期是π其中正确的是( )
)(k∈Z)上是减函数 ⑤最小正周期是π其中正确的是( )
A.①②③
B.②④⑤
C.②④
D.③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛中获胜的事件是独立的,并且获胜的概率均为 ![]() .
.
(1)求这支篮球队首次获胜前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好获胜3场的概率;
(3)求这支篮球队在6场比赛中获胜场数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD. 
(1)求证:PQ∥平面SAD;
(2)求证:SQ⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D表示不等式组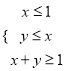 所确定的平面区域,在D内存在 无数个点落在y=a(x+2)上,则a的取值范围是 ( )
所确定的平面区域,在D内存在 无数个点落在y=a(x+2)上,则a的取值范围是 ( )
A. R B. (![]() ,1) C. (0,
,1) C. (0, ![]() ) D. (﹣∞,0]∪[
) D. (﹣∞,0]∪[![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com