Question

已知B、C是两个定点，|BC|=6,且△ABC的周长等于16，求顶点A的轨迹方程.

Answer 1

思路分析：本题中已知三角形的周长及其中一条边的长度，因此可以求出另两条边的长度和，画出图形观察可以发现，点A的轨迹方程是一个椭圆.

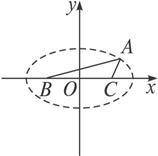
解：如图，建立坐标系，使x轴经过点B、C,原点O与BC的中点重合.

由已知|AB|+|AC|+|BC|=16,|BC|=6，有|AB|+|AC|=10，

即点A的轨迹是椭圆，且2c=6，2a=16-6=10.

∴c=3，a=5，b²=5²-3²=16.

但当点A在直线BC上，即y=0时，A、B、C三点不能构成三角形；

∴点A的轨迹方程是=1(y≠0)

    方法点拨 在解析几何里，求符合某种条件的点的轨迹方程，要建立适当的坐标系.为建立适当的坐标系，常常需要画出草图.求出曲线的方程后，要注意检查一下方程的曲线上的点是否都符合题意，如果有不符合题意的点，应在所得方程后注明限制条件.