
(1)甲、乙、丙三人在同一次计算机考试中谁获得“合格证书”的可能性最大?
(2)求这三人计算机考试都获得“合格证书”的概率;
(3)(理)用ξ表示甲、乙、丙三人在理论考试中合格的人数,求ξ的分布列和数学期望Eξ.
(文)求甲、乙、丙三人在理论考试中至少有两人合格的概率;
答案:记“甲理论考试合格”为事件A1,“乙理论考试合格”为事件A2,“丙理论考试合格”为事件A3,记![]() 为Ai的对立事件,i=l,2,3;记“甲上机考试合格”为事件B1,“乙上机考试合格”为事件B2,“丙上机考试合格”为事件B3.
为Ai的对立事件,i=l,2,3;记“甲上机考试合格”为事件B1,“乙上机考试合格”为事件B2,“丙上机考试合格”为事件B3.
(1)记“甲计算机考试获得合格证书”为事件A,记“乙计算机考试获得合格证书”为事件B,记“丙计算机考试获得合格证书”为事件C,则P(A)=![]() ,
,
P(B)=![]() ,P(C)=
,P(C)=![]() ,
,
有P(B)>P(C)>P(A),
故丙获得“合格证书”可能性最大.
(2)记“三人该课程考核都合格”为事件D.
P(D)=P[(A1B1)·(A2B2)·(A3B3)]
=P(A1B1)·P(A2B2)·P(A3B3)
=P(A1)P(B1)P(A2)P(B2)P(A3)P(B3)
所以,这三人该课程考核都合格的概率为![]() .
.
(3)(理)用ξ表示甲、乙、丙三人在理论考试中的合格人数,则ξ可以取0,1,2,3,故ξ的分布列如下:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.
(文)记“理论考试中至少有两人合格”为事件E,记![]() 为E的对立事件
为E的对立事件
P(E)=P(A1A2![]() +A1
+A1![]() A3+
A3+![]() A2A3+A1A2A3)=+P(A1A2
A2A3+A1A2A3)=+P(A1A2![]() )+P(A1
)+P(A1![]() A3)+P(
A3)+P(![]() A2A3)=P(A1A2A3)=
A2A3)=P(A1A2A3)=![]()
所以,理论考试中至少有两人合格的概率为![]() .
.


科目:高中数学 来源: 题型:
| 3 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 9 |
| 10 |
| 5 |
| 6 |
| 7 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三下学期开学考试理科数学试卷(解析版) 题型:选择题
计算机考试分理论考试与实际操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格“并颁发”合格证书“.甲、乙、丙三人在理论考试中“合格”的概率依次为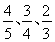 ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为 ,所有考试是否合格相互之间没有影响。
,所有考试是否合格相互之间没有影响。
(1)假设甲、乙、丙3人同时进行理论与实际操作两项考试,谁获得“合格证书”的可能性大?
(2)求这3人进行理论与实际操作两项考试后,恰有2人获得“合格证书”的概率;
(3)用X表示甲、乙、丙3人计算机考试获“合格证书”的人数,求X的分布列和数学期望EX。
查看答案和解析>>
科目:高中数学 来源:2012年北京市顺义区高考数学二模试卷(理科)(解析版) 题型:解答题
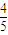 、
、 、
、 ,在实际操作考试中“合格”的概率依次为:
,在实际操作考试中“合格”的概率依次为: 、
、 、
、 ,所有考试是否合格相互之间没有影响.
,所有考试是否合格相互之间没有影响.查看答案和解析>>
科目:高中数学 来源:2012年北京市顺义区高考数学一模试卷(理科)(解析版) 题型:解答题
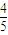 、
、 、
、 ,在实际操作考试中“合格”的概率依次为:
,在实际操作考试中“合格”的概率依次为: 、
、 、
、 ,所有考试是否合格相互之间没有影响.
,所有考试是否合格相互之间没有影响.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com