
【题目】已知函数![]() .
.
(1)求f(x)的定义域和值域;
(2)判断f(x)的奇偶性与单调性;
(3)解关于x的不等式f(x2﹣2x+2)+f(﹣5)<0.
【答案】(1)定义域R,值域为![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)将函数看作方程,解得![]() ,再由2x>0,解得y的范围,即为所求;(2)函数f(x)的定义域为R,由f(﹣x)=﹣f(x),推出f(x)是奇函数;利用函数单调性的定义证明函数f(x)在(-∞,+∞)上单调递增;(3)利用f(x)为奇函数把不等式转化为f(x2﹣2x+2)<f(5),再根据其单调性即可得到不等式的解集.
,再由2x>0,解得y的范围,即为所求;(2)函数f(x)的定义域为R,由f(﹣x)=﹣f(x),推出f(x)是奇函数;利用函数单调性的定义证明函数f(x)在(-∞,+∞)上单调递增;(3)利用f(x)为奇函数把不等式转化为f(x2﹣2x+2)<f(5),再根据其单调性即可得到不等式的解集.
(1)f(x)的定义域是R,令y=![]() ,得2x=﹣
,得2x=﹣![]() .
.
∵2x>0,∴﹣![]() >0,解得﹣1<y<1.
>0,解得﹣1<y<1.
∴f(x)的值域为{y|﹣1<y<1};
(2)∵f(﹣x)=![]() =
=![]() =﹣f(x),∴f(x)是奇函数.
=﹣f(x),∴f(x)是奇函数.
∵f(x)=![]() =1﹣
=1﹣![]() ,在R上任取x1,x2,且x1<x2,
,在R上任取x1,x2,且x1<x2,
f(x1)﹣f(x2)=![]() =
=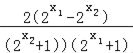 ,
,
∵x1<x2,∴![]() ,
,![]() (2x1+1)>0,
(2x1+1)>0,
即有f(x1)<f(x2),则f(x)在R上是增函数.
(3)由(2)得f(x)是奇函数,且f(x)在R上是增函数.
则f(x2﹣2x+2)+f(﹣5)<0即为f(x2﹣2x+2)<﹣f(﹣5)=f(5),
得x2﹣2x+2<5,即有x2﹣2x﹣3<0,
解得﹣1<x<3,则不等式解集为(﹣1,3).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1) 求实数![]() 的值;
的值;
(2) 判断并用定义证明该函数在定义域![]() 上的单调性;
上的单调性;
(3) 若方程![]() 在
在![]() 内有解,求实数
内有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某超市的一种小商品在过去近20天内的日销售量(件)与价格(元)均为时间t(天)的函数,且日销售量(件)近似函数g(t)=80-2t,价格(元)近似满足函数关系式为
f(t)=20-![]() |t-10|.
|t-10|.
(1)试写出该种商品的日销售额y与时间t(0≤t≤20)的函数表达式;
(2)求该种商品的日销售额y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线M的方程为ρ2(1+sin2θ)=1.
(t为参数),在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线M的方程为ρ2(1+sin2θ)=1.
(1)求曲线M的直角坐标方程;
(2)若直线l与曲线M只有一个公共点,求倾斜角α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() ,其中
,其中![]() 的公差不为
的公差不为![]() .设
.设![]() 是数列
是数列![]()
的前![]() 项和.若
项和.若![]() 、
、![]() 、
、![]() 是数列
是数列![]() 的前
的前![]() 项,且
项,且![]() .
.
(Ⅰ)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 为等差数列,求实数
为等差数列,求实数![]() ;
;
(Ⅲ)构造数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,
,…,
若该数列前![]() 项和
项和![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com