练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，a，b，c分别为角A，B，C所对的边，角C是钝角，且sinB= ．
    （1）求角C的值；
    （2）若b=2，△ABC的面积为 ，求c的值．

    【答案】
    （1）解：由sinB= 得2csinB=b，由正弦定理得：2sinCsinB=sinB，

    所以sinB（2sinC﹣1）=0，

    因为sinB≠0，

    所以sinC= ，

    因为C是钝角，

    所以C= ．


    （2）解：因为S= absinC= a= ，a=2 ，

    由余弦定理得c2=a2+b2﹣2abcosC=12+4﹣2× （﹣ ）=28，

    所以c=2 ，即c的值为2 ．


    【解析】（1）由正弦定理化简已知可得sinB（2sinC﹣1）=0，由sinB≠0解得sinC= ，结合C是钝角，即可解得C的值．（2）由已知及三角形面积公式可求a的值，由余弦定理即可解得c的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一辆汽车在某段路程中的行驶速率与时间的关系如图所示．
    （1）求图中阴影部分的面积，并说明所求面积的实际含义；
    （2）假设这辆汽车在行驶该段路程前里程表的读数是8018km，试求汽车在行驶这段路程时里程表读数s（km）与时间t （h）的函数解析式，并作出相应的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现代城市大多是棋盘式布局（如上海道路几乎都是东西和南北走向）．在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离（位移），而是实际路程（如图）．在直角坐标平面内，我们定义A（x1 ， y1）、B（x2 ， y2）两点间的“直角距离”为：D（AB）=|x1﹣x2|+|y1﹣y2|．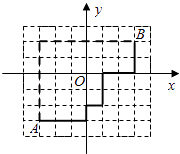

    （1）在平面直角坐标系中，写出所有满足到原点的“直角距离”
    为2的“格点”的坐标；（格点指横、纵坐标均为整数的点）
    （2）定义：“圆”是所有到定点“直角距离”为定值的点组成的图形，点A（1，3），B（1，1），C（3，3），求经过这三个点确定的一个“圆”的方程，并画出大致图象；
    （3）设P（x，y），集合B表示的是所有满足D（PO）≤1的点P所组成的集合，
    点集A={（x，y）|﹣1≤x≤1，﹣1≤y≤1}，
    求集合Q={（x，y）|x=x1+x2 ， y=y1+y2 ， （x1 ， y1）∈A，（x2 ， y2）∈B}所表示的区域的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知锐角△ABC的三内角A，B，C所对的边分别是a，b，c，且2csinB= b．
    （1）求角C的大小；
    （2）若边c=1，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{bn}的前n项和是Sn ， 且bn=1﹣2Sn ， 又数列{an}、{bn}满足点{an ， 3 }在函数y=（ ）x的图象上．
    （1）求数列{an}，{bn}的通项公式；
    （2）若cn=anbn+ ，求数列{an}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2+y2﹣2x+4y﹣4=0，是否存在斜率为1的直线l，使l被圆C截得的弦长AB为直径的圆过原点，若存在求出直线的方程l，若不存在说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列结论： ①已知函数f（x）是定义在R上的奇函数，若f（﹣1）=2，f（﹣3）=﹣1，则f（3）＜f（﹣1）；
    ②函数y=log （x2﹣2x）的单调递增减区间是（﹣∞，0）；
    ③已知函数f（x）是奇函数，当x≥0时，f（x）=x2 ， 则当x＜0时，f（x）=﹣x2；
    ④若函数y=f（x）的图象与函数y=ex的图象关于直线y=x对称，则对任意实数x，y都有f（xy）=f（x）+f（y）．
    则正确结论的序号是（请将所有正确结论的序号填在横线上）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 是奇函数，f（x）=lg（10x+1）+bx是偶函数．
    （1）求a+b的值．
    （2）若对任意的t∈[0，+∞），不等式g（t2﹣2t）+g（2t2﹣k）＞0恒成立，求实数k的取值范围．
    （3）设 ，若存在x∈（﹣∞，1]，使不等式g（x）＞h[lg（10a+9）]成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A=[﹣1，3]，B=[m，m+6]，m∈R．
    （1）当m=2时，求A∩RB；
    （2）若A∪B=B，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案