
【题目】为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租.该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆.为了便于结算,每辆自行车的日租金![]() (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用![]() (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(1)求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,且满足
两点,且满足![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点.
两点. ![]() 为坐标原点,若
为坐标原点,若![]() 的面积为
的面积为![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是直线
是直线![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() 分别为该椭圆的左右焦点,设
分别为该椭圆的左右焦点,设![]() 取得最小值时椭圆为
取得最小值时椭圆为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)已知![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的两点,
轴对称的两点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,试判断
,试判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元)
(单位:元)

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|-1≤x≤2},B={x|m-1≤x≤2m+1},已知BA.
(1)当x∈N时,求集合A的子集的个数;
(2)求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
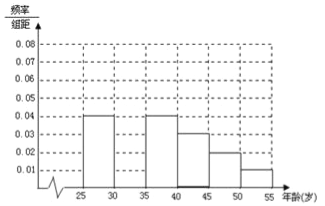
(1)补全频率分布直方图并求![]() 的值(直接写结果);
的值(直接写结果);
(2)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在![]() 岁的概率.
岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,圆
,圆![]() 的圆心在圆
的圆心在圆![]() 的内部,且直线
的内部,且直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() .点
.点![]() 为圆
为圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求证:![]() 为定值;
为定值;
(3)当![]() 取得最大值时,求
取得最大值时,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com