
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
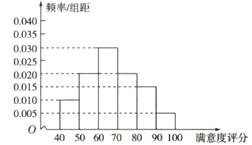
【题目】已知函数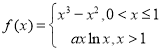 ,(
,(![]() ).
).
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设点![]() ,
,![]() 是函数
是函数![]() 图象的不同两点,其中
图象的不同两点,其中![]() ,
,![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,且函数
,且函数![]() 在点
在点![]() 切线的斜率为
切线的斜率为![]() ,若存在,请求出
,若存在,请求出![]() 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市交通管理有关部门对![]() 年参加驾照考试的
年参加驾照考试的![]() 岁以下的学员随机抽取
岁以下的学员随机抽取![]() 名学员,对他们的科目三(道路驾驶)和科目四(安全文明相关知识)进行两轮测试,并把两轮成绩的平均分作为该学员的抽测成绩,记录数据如下:
名学员,对他们的科目三(道路驾驶)和科目四(安全文明相关知识)进行两轮测试,并把两轮成绩的平均分作为该学员的抽测成绩,记录数据如下:
学员编号 |
|
|
|
|
|
|
|
|
|
|
科目三成绩 |
|
|
|
|
|
|
|
|
|
|
科目四成绩 |
|
|
|
|
|
|
|
|
|
|
(1)从![]() 年参加驾照考试的
年参加驾照考试的![]() 岁以下学员中随机抽取一名学员,估计这名学员抽测成绩大于或等于
岁以下学员中随机抽取一名学员,估计这名学员抽测成绩大于或等于![]() 分的概率;
分的概率;
(2)根据规定,科目三和科目四测试成绩均达到![]() 分以上(含
分以上(含![]() 分)才算合格,从抽测的
分)才算合格,从抽测的![]() 到
到![]() 号学员中任意抽取两名学员,记
号学员中任意抽取两名学员,记![]() 为抽取学员不合格的人数,求
为抽取学员不合格的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:中位数为2,极差为5; 乙地:总体平均数为2,众数为2;
丙地:总体平均数为1,总体方差大于0; 丁地:总体平均数为2,总体方差为3.
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )

A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图(如图)和B地区用户满意度评分的频数分布表.
B地区用户满意度评分的频数分布表
满意度评分分组 |
|
|
|
|
|
频数 | 2 | 8 | 14 | 10 | 6 |
在图中作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).
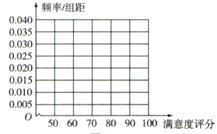
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 9 | 10 | 11 | 8 | 12 |
发芽数 | 38 | 30 | 24 | 41 | 17 |
利用散点图,可知![]() 线性相关。
线性相关。
(1)求出![]() 关于
关于![]() 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差![]() ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
(2)若从4月1日![]() 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
(公式: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com