
【题目】如图,正方形![]() 中,
中, ![]() ,
, ![]() 与
与![]() 交于
交于![]() 点,现将
点,现将![]() 沿
沿![]() 折起得到三棱锥
折起得到三棱锥![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
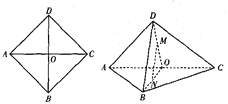
(1)求证: ![]() ;
;
(2)若三棱锥![]() 的最大体积为
的最大体积为![]() ,当三棱锥
,当三棱锥![]() 的体积为
的体积为![]() ,且二面角
,且二面角![]() 为锐角时,求二面角
为锐角时,求二面角![]() 的正弦值.
的正弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额如下表:
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图,观察散点图,说明两个变量是否线性相关;
(2)用最小二乘法计算利润额y对销售额x的线性回归方程;
(3)当销售额为4千万元时,估计利润额的大小.
(参考公式: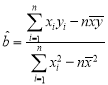 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】墙上有一壁画,最高点![]() 处离地面
处离地面![]() 米,最低点
米,最低点![]() 处离地面
处离地面![]() 米,距离墙
米,距离墙![]() 米处设有防护栏,观察者从离地面高
米处设有防护栏,观察者从离地面高![]() 米的
米的![]() 处观赏它.
处观赏它.
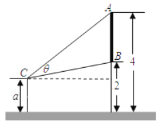
(1)当![]() 时,观察者离墙多远时,视角
时,观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() ,视角
,视角![]() 的正切值恒为
的正切值恒为![]() ,观察者离墙的距离应在什么范围内?
,观察者离墙的距离应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 内有一点
内有一点![]() ,
,![]() 为圆
为圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线与
的垂直平分线与![]() 的连线交于点
的连线交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程.
的轨迹方程.
(Ⅱ)若动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点,且以
两点,且以![]() 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点![]() .问是否存在一个定圆与动直线
.问是否存在一个定圆与动直线![]() 总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
总相切.若存在,求出该定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)写出函数![]() 的单调递减区间(无需证明) ;
的单调递减区间(无需证明) ;
(Ⅲ)若实数![]() 满足
满足![]() ,则称
,则称![]() 为
为![]() 的二阶不动点,求函数
的二阶不动点,求函数![]() 的二阶不动点的个数.
的二阶不动点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对某热播电视剧的喜爱程度,某电视台在甲、乙两地各随机抽取了8名观众作问卷调查,得分统计结果如图所示:
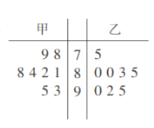
(1)计算甲、乙两地被抽取的观众问卷的平均得分;
(2)计算甲、乙两地被抽取的观众问卷得分的方差;
(3)若从甲地被抽取的8名观众中再邀请2名进行深入调研,求这2名观众中恰有1人的问卷调查成绩在90分以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间的一台机床生产出一批零件,现从中抽取8件,将其编为![]() ,
, ![]() ,…,
,…, ![]() ,测量其长度(单位:
,测量其长度(单位: ![]() ),得到下表中数据:
),得到下表中数据:
编号 |
|
|
|
|
|
|
|
|
长度 | 1.49 | 1.46 | 1.51 | 1.51 | 1.53 | 1.51 | 1.47 | 1.51 |
其中长度在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)从上述8个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取2个.
①用零件的编号列出所有可能的抽取结果;
②求这2个零件长度相等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com