
分析 由条件知,Aα=2α,从而$\left\{\begin{array}{l}2+a=4\\-2+b=2\end{array}\right.$,由此能求出a,b的值.
解答 解:∵矩阵A=$[\begin{array}{l}{1}&{a}\\{-1}&{b}\end{array}]$的一个特征值为2,其对应的一个特征向量为a=$[\begin{array}{l}{2}\\{1}\end{array}]$,
∴由条件知,Aα=2α,即$[{\begin{array}{l}1&a\\{-1}&b\end{array}}][{\begin{array}{l}2\\ 1\end{array}}]=2[{\begin{array}{l}2\\ 1\end{array}}]$,即$[{\begin{array}{l}{2+a}\\{-2+b}\end{array}}]=[{\begin{array}{l}4\\ 2\end{array}}]$,…(6分)
∴$\left\{\begin{array}{l}2+a=4\\-2+b=2\end{array}\right.$,解得$\left\{\begin{array}{l}a=2\\ b=4.\end{array}\right.$
∴a,b的值分别为2,4.…(10分)
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意特征向量的性质的合理运用.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
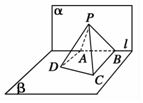 如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C,D是平面β内的两点,且 DA⊥l,CB⊥l,DA=2,AB=4,CB=4,P是平面α上的一动点,且直线 PD,PC与平面α所成角相等,则二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.
如图,已知平面α⊥β,α∩β=l,A,B是直线l上的两点,C,D是平面β内的两点,且 DA⊥l,CB⊥l,DA=2,AB=4,CB=4,P是平面α上的一动点,且直线 PD,PC与平面α所成角相等,则二面角 P-BC-D的余弦值的最小值是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com