
【题目】已知,正方体ABCD-A1B1C1D1中,点E,F分别为D1C1,C1B1的中点,
AC∩BD=P,A1C1∩EF=Q.求证:
(1)D,B,E,F四点共面.
(2)若A1C交平面BDEF于点R,则P,Q,R三点共线.
科目:高中数学 来源: 题型:
【题目】已知直线y=-![]() x+5的倾斜角是直线l的倾斜角的大小的5倍,分别求满足下列条件的直线l的方程.
x+5的倾斜角是直线l的倾斜角的大小的5倍,分别求满足下列条件的直线l的方程.
(1)过点P(3,-4);
(2)在x轴上截距为-2;
(3)在y轴上截距为3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l1的参数方程为 ![]() ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为  ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣ ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的公差d>0,且a1>0,记Tn= ![]() +
+ ![]() ++
++ ![]() .
.
(1)用a1、d分别表示T1、T2、T3 , 并猜想Tn;
(2)用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了解高中学生的性别和喜欢打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:
喜欢打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为 ![]()
(Ⅰ)请将上述列联表补充完整;
(Ⅱ)判断是否有99.5%的把握认为喜欢打篮球与性别有关?
附:K2= ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥平面ABC,AE⊥PB,AB⊥BC,AF⊥PC,PA=AB=BC.
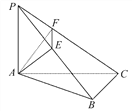
(1)求证:平面AEF⊥平面PBC.
(2)求二面角P-BC-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(2,2),N(5,-2),点P在x轴上,分别求满足下列条件的点P的坐标.
(1)∠MOP=∠OPN(O是坐标原点).
(2)∠MPN是直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为1的正方体ABCD-A1B1C1D1中,点E,F,M分别是AB,AD,AA1的中点,又P,Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设平面MEF∩平面MPQ=l,则下列结论中不成立的是 ( )
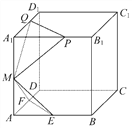
A. l∥平面ABCD
B. l⊥AC
C. 平面MEF与平面MPQ不垂直
D. 当x变化时,l不是定直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2
(t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2 ![]() cosθ. (Ⅰ)求C2与C3交点的直角坐标;
cosθ. (Ⅰ)求C2与C3交点的直角坐标;
(Ⅱ)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com