
【题目】某农科所对冬季昼夜温差大小与某反季大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了2015年12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如表:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x(℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() bx+a;
bx+a;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?
 ,
,![]() .
.
 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
【题目】瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(-1,3),点C(4,-2),且其“欧拉线”与圆M:![]() 相切,则下列结论正确的是( )
相切,则下列结论正确的是( )
A.圆M上点到直线![]() 的最小距离为2
的最小距离为2![]()
B.圆M上点到直线![]() 的最大距离为3
的最大距离为3![]()
C.若点(x,y)在圆M上,则![]() 的最小值是
的最小值是![]()
D.圆![]() 与圆M有公共点,则a的取值范围是
与圆M有公共点,则a的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应德智体美劳的教育方针,唐徕回中高一年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如下:
每分钟跳绳个数 |
|
|
|
| 185以上 |
得分 | 16 | 17 | 18 | 19 | 20 |
年级组为了了解学生的体质,随机抽取了100名学生,统计了他的跳绳个数,并绘制了如下样本频率直方图:
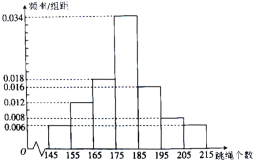
(1)现从这100名学生中,任意抽取2人,求两人得分之和小于35分的概率(结果用最简分数表示);
(2)若该校高二年级2000名学生,所有学生的一分钟跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() ,
,![]() 为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
①估计每分钟跳绳164个以上的人数(四舍五入到整数)
②若在全年级所有学生中随机抽取3人,记每分钟跳绳在179个以上的人数为![]() ,求
,求![]() 的分布列和数学期望与方差.
的分布列和数学期望与方差.
(若随机变量![]() 服从正态分布
服从正态分布![]() 则
则![]() ,
,![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AD.M,N分别是AB,PC的中点.
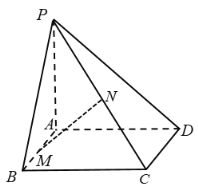
(1)求证:MN//平面PAD;
(2)求证:MN⊥平面PCD;
(3)求二面角B—PC—D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:
(1)A:取出的两球都是白球;
(2)B:取出的两球1个是白球,另1个是红球.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下几个命题中:
①线性回归直线方程![]() 恒过样本中心
恒过样本中心![]() ;
;
②用相关指数![]() 可以刻画回归的效果,值越小说明模型的拟合效果越好;
可以刻画回归的效果,值越小说明模型的拟合效果越好;
③随机误差是引起预报值![]() 和真实值
和真实值![]() 之间存在误差的原因之一,其大小取决于随机误差的方差;
之间存在误差的原因之一,其大小取决于随机误差的方差;
④在含有一个解释变量的线性模型中,相关指数![]() 等于相关系数
等于相关系数![]() 的平方.
的平方.
其中真命题为 _________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
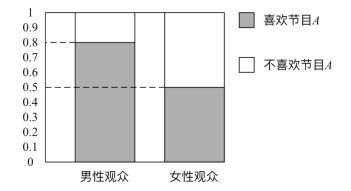
根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 | 60 |
附: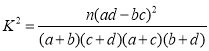
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.则下列结论中表述不正确的是( )
(单位:亿元)的折线图.则下列结论中表述不正确的是( )
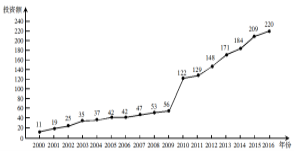
A. 从2000年至2016年,该地区环境基础设施投资额逐年增加;
B. 2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;
C. 2012年该地区基础设施的投资额比2004年的投资额翻了两番 ;
D. 为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为![]() )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型![]() ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com