
【题目】在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:命题“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]() =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
【答案】(1)见解析;
(2)见解析.
【解析】
(1)直线方程与抛物线方程联立,消去![]() 后利用韦达定理判断
后利用韦达定理判断![]() 的值是否为3,从而确定此命题是否为真命题;
的值是否为3,从而确定此命题是否为真命题;
(2)根据四种命题之间的关系写出该命题的逆命题,然后再利用直线与抛物线的位置关系知识来判断其真假.
(1)证明:设过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,
,
当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
此时,直线![]() 与抛物线相交于
与抛物线相交于![]() ,
,
所以![]() ,
,
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,其中
,其中![]() ,
,
 ,得
,得![]() ,
,
则![]() ,
,
又因为![]() ,
,
所以![]() ,
,
综上所述,命题“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]() =3”是真命题;
=3”是真命题;
(2)逆命题是:“设直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点,如果
相交于A、B两点,如果![]() =3,那么该直线过点
=3,那么该直线过点![]() ”,该命题是假命题,
”,该命题是假命题,
例如:取抛物线上的点![]() ,此时
,此时![]() =3,直线AB的方程为
=3,直线AB的方程为![]() ,而T(3,0)不在直线AB上.
,而T(3,0)不在直线AB上.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
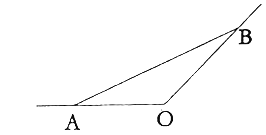
【题目】如图所示,某城市有一条从正西方AO通过市中心O后向东北OB的公路,现要修一条地铁L,在OA,OB上各设一站A,B,地铁在AB部分为直线段,现要求市中心O与AB的距离为![]() ,设地铁在AB部分的总长度为
,设地铁在AB部分的总长度为![]() .
.
![]() 按下列要求建立关系式:
按下列要求建立关系式:
![]() 设
设![]() ,将y表示成
,将y表示成![]() 的函数;
的函数;
![]() 设
设![]() ,
,![]() 用m,n表示y.
用m,n表示y.
![]() 把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥O﹣ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.

(1)求异面直线BE与AC所成角的余弦值;
(2)求直线BE和平面ABC的所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组在科学馆的帕斯卡三角仪器前进行探究实验.如图所示,每次使一个实心小球从帕斯卡三角仪器的顶部入口落下,当它在依次碰到每层的菱形挡板时,会等可能地向左或者向右落下,在最底层的7个出口处各放置一个容器接住小球,该小组连续进行200次试验,并统计容器中的小球个数得到柱状图:
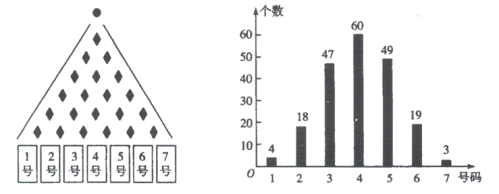
(Ⅰ)用该实验来估测小球落入4号容器的概率,若估测结果的误差小于![]() ,则称该实验是成功的.试问:该兴趣小组进行的实验是否成功?(误差
,则称该实验是成功的.试问:该兴趣小组进行的实验是否成功?(误差![]() )
)
(Ⅱ)再取3个小球进行试验,设其中落入4号容器的小球个数为![]() ,求
,求![]() 的分布列与数学期望.(计算时采用概率的理论值)
的分布列与数学期望.(计算时采用概率的理论值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数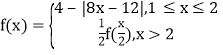 及如下的4个命题:
及如下的4个命题:
![]() 关于x的方程
关于x的方程![]() 有
有![]() 个不同的零点;
个不同的零点;
![]() 对于实数
对于实数![]() ,不等式
,不等式![]() 恒成立;
恒成立;
![]() 在
在![]() 上,方程
上,方程![]() 有5个零点;
有5个零点;
![]() 时,函数
时,函数![]() 的图象与x轴图成的形的面积是4.
的图象与x轴图成的形的面积是4.
则以上命题正确的为______![]() 把正确命题前的序号填在横线上
把正确命题前的序号填在横线上![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com